题目内容
若函数f(x)在R上可导,且满足f(x)<xf′(x),则( )
| A、2f(1)<f(2) |
| B、2f(1)>f(2) |
| C、2f(1)=f(2) |
| D、f(1)=f(2) |
考点:导数的运算
专题:导数的概念及应用
分析:根据条件f(x)<xf′(x)可构造函数g(x)=
,然后得到函数的单调性,从而得到所求.
| f(x) |
| x |
解答:
解:设g(x)=
,
则g′(x)=
,
∵f(x)<xf′(x),
∴g′(x)>0,
即g(x)在(0,+∞)上单调递增,
∴
<
,
即2f(1)<f(2)
故选:A.
| f(x) |
| x |
则g′(x)=
| xf′(x)-f(x) |
| x2 |
∵f(x)<xf′(x),
∴g′(x)>0,
即g(x)在(0,+∞)上单调递增,
∴
| f(1) |
| 1 |
| f(2) |
| 2 |
即2f(1)<f(2)
故选:A.
点评:本题主要考查了导数除法的运算法则,以及利用构造法是解题的关键,同时考查了运算求解的能力,属于基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
侧棱和底面垂直的三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AC=1,BC=3,∠ACB=60°,C1C=2
,则球O的表面积为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若不等式|x+a|<6的解集为(-1,11),则实数a等于( )
| A、-1 | B、-7 | C、7 | D、-5 |
下列函数中,在(0,2)内有零点且单调递增的是( )
| A、y=2x-2 | ||
B、y=log
| ||
| C、y=|x|-3 | ||
| D、y=-x3 |
已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则A∪B=( )
| A、{2} |
| B、{2,3,4} |
| C、{1,2,3,4} |
| D、{0,2,3,4} |
西华三高学生会随机对高二文科班的50名学生进行了上课是否睡觉的调查,数据如下表:
根据表中数据得到k=
≈5.059,则认为带手机与上课睡觉有关系的把握大约为( )
| 上课常睡觉 | 上课不睡觉 | 总数 | |
| 带手机 | 18 | 9 | 27 |
| 没带手机 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |
| 50×(18×15-8×9)2 |
| 27×23×24×26 |
| A、90% | B、95% |
| C、97.5% | D、无充分根据 |
已知i为虚数单位,则i(1+i)2=( )
| A、2i | B、-2i | C、2 | D、-2 |
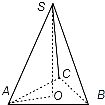 如图,在三棱锥S-ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为( )
如图,在三棱锥S-ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为( )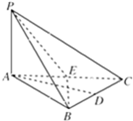 如图,三棱锥P-ABC中,PA⊥底面ABC,△ABC为正三角形,D、E分别是BC、CA的中点.
如图,三棱锥P-ABC中,PA⊥底面ABC,△ABC为正三角形,D、E分别是BC、CA的中点.