题目内容
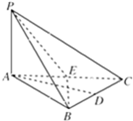如图，三棱锥P-ABC中，PA⊥底面ABC，△ABC为正三角形，D、E分别是BC、CA的中点．（1）证明：平面PBE⊥平面PAC
（2）试在BC上找一点F，使AD∥平面PEF？并说明理由．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）由线面垂直得PA⊥BE，由正三角形性质得BE⊥CA，由此能证明面PBE⊥面PAC．
（2）取CD中点F，则F就是使AD∥平面PEF的点，可利用三角形中位线定理证明．
（2）取CD中点F，则F就是使AD∥平面PEF的点，可利用三角形中位线定理证明．
解答：
（1）证明：∵PA⊥底面ABC，∴PA⊥BE，
又∵△ABC是正三角形，且E为AC的中点，
∴BE⊥CA，又PA∩CA=A，
∴BE⊥平面PAC，
∵BE?平面PAC，∴面PBE⊥面PAC．
（2）解：取CD中点F，则F就是使AD∥平面PEF的点，
∵E、F分别为CA，CD的中点，
∴EF∥AD，
又EF?平面PEF，AD不包含于平面PEF，
∴AD∥平面PEF．
又∵△ABC是正三角形，且E为AC的中点，
∴BE⊥CA，又PA∩CA=A，
∴BE⊥平面PAC，
∵BE?平面PAC，∴面PBE⊥面PAC．
（2）解：取CD中点F，则F就是使AD∥平面PEF的点，
∵E、F分别为CA，CD的中点，
∴EF∥AD，
又EF?平面PEF，AD不包含于平面PEF，
∴AD∥平面PEF．
点评：本题考查平面与平面垂直的证明，考查直线与平面平行的点的位置的确定，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
春雨教育同步作文系列答案
相关题目
若函数f（x）在R上可导，且满足f（x）＜xf′（x），则（ ）
| A、2f（1）＜f（2） |
| B、2f（1）＞f（2） |
| C、2f（1）=f（2） |
| D、f（1）=f（2） |
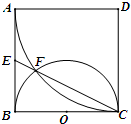如图，正方形ABCD边长为2，以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F，连结CF并延长交AB于点E．
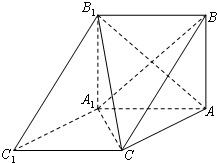如图，三棱柱ABC-A1B1C1中，BA⊥平面AA1C1C，AB=2
如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，AD垂直于AB和DC，侧棱SA⊥底面ABCD，且SA=2，AD=DC=1，点E在SD上，且AE⊥SD．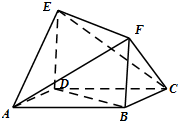
如图所示的多面体中，ABCD是菱形，BDEF是矩形，ED⊥面ABCD，