题目内容
已知实数x≤y≤z,且xy+xz+yz=1,则xz的上界为 .
考点:基本不等式在最值问题中的应用
专题:不等式的解法及应用
分析:由题意可得xz≤yz,利用不等式放缩可得yz≥
,即可得出结论.
| 1 |
| 3 |
解答:
解:∵x≤y≤z,且xy+xz+yz=1,
∵xy+yz=(x+z)y>zx,
∴1=xy+xz+yz>2xz,∴xz<
.
故答案为:
.
∵xy+yz=(x+z)y>zx,
∴1=xy+xz+yz>2xz,∴xz<
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查不等式的性质及放缩法求函数的最值等知识,属于基础题.

练习册系列答案
相关题目
已知△ABC的角A,B,C所对应的边分别为a,b,c,且cosB=
,a=10,S△ABC=42,则b+
=( )
| 4 |
| 5 |
| a |
| sinA |
A、
| ||||
| B、16 | ||||
C、8
| ||||
D、16
|
在二项式(2
+
)n的展开式中,前三项的系数成等差数列,则该二项式展开式中x-2项的系数为( )
| x |
| 1 | |||
|
| A、1 | B、4 | C、8 | D、16 |
已知某几何体的三视图如图所示(单位cm),则此几何体的体积为( )
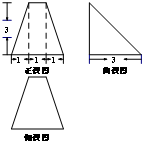

A、
| ||
B、
| ||
| C、16cm3 | ||
| D、12cm3 |
已知△ABC的三个内角A,B,C所对的边分别为a,b,c,且acosC+
c=b则角A的大小为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|