题目内容
已知
，
是平面内两个不共线的非零向量，
=2
+
，
=-
+λ
，
=-2
+
，且A，E，C三点共线．
（1）求实数λ的值；若
=（2，1），
=（2，-2），求
的坐标；
（2）已知点D（3，5），在（1）的条件下，若ABCD四点构成平行四边形，求点A的坐标．
| e1 |
| e2 |
| AB |
| e1 |
| e2 |
| BE |
| e1 |
| e2 |
| EC |
| e1 |
| e2 |
（1）求实数λ的值；若
| e1 |
| e2 |
| BC |
（2）已知点D（3，5），在（1）的条件下，若ABCD四点构成平行四边形，求点A的坐标．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：本题（1）通过几何法将向量转化为两向量的和，再将所得向量坐标化，即可得正确结论；（2）由已知几何条件得到向量间关系，再坐标化得到A点的坐标，即本题答案．
解答：
解：（1）∵
=
+
=(2
+
)+(-
+λ
)=
+(1+λ)
，
∵A，E，C三点共线，∴存在实数k，使得
=k
．
即
+(1+λ)
=k(-2
+
)，
得(1+2k)
=(k-1-λ)
．
∵
，
是平面内两个不共线的非零向量，
∴
，
解得k=-
，λ=-
．
∴
=
+
=-3
-
=(-6，-3)+(-1，1)=(-7，-2)．
（2）∵A、B、C、D四点构成平行四边形，
∴
=
．
设A（x，y），则
=(3-x，5-y)，
又
=(-7，-2)，
∴
，
解得
，
∴点A（10，7）．
| AE |
| AB |
| BE |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
∵A，E，C三点共线，∴存在实数k，使得
| AE |
| EC |
即
| e1 |
| e2 |
| e1 |
| e2 |
得(1+2k)
| e1 |
| e2 |
∵
| e1 |
| e2 |
∴
|
解得k=-
| 1 |
| 2 |
| 3 |
| 2 |
∴
| BC |
| BE |
| EC |
| e1 |
| 1 |
| 2 |
| e2 |
（2）∵A、B、C、D四点构成平行四边形，
∴
| AD |
| BC |
设A（x，y），则
| AD |
又
| BC |
∴
|
解得
|
∴点A（10，7）．
点评：本题考查的是平面向量的坐标运算，有一定的思维量，属于中档题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
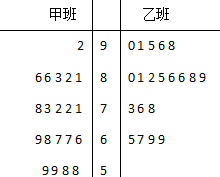我市某校某数学老师这学期分别用m，n两种不同的教学方式试验高一甲、乙两个班（人数均为60人，入学数学平均分和优秀率都相同，勤奋程度和自觉性都一样）．现随机抽取甲、乙两班各20名的数学期末考试成绩，并作出茎叶图如图所示．