题目内容
已知f(x)=ex-1-x-ax2.
(1)当a=0时,讨论f(x)的单调性;
(2)若对?x≥0,恒有f(x)≥0,求a的范围.
(1)当a=0时,讨论f(x)的单调性;
(2)若对?x≥0,恒有f(x)≥0,求a的范围.
考点:利用导数研究函数的单调性,函数恒成立问题
专题:导数的概念及应用,导数的综合应用
分析:(1)将a=0代入并求导,分析定义域各区间上导数的符号,进而根据导函数符号与原函数单调性的关系,可得结论.
(2)先证明ex≥1+x可得不等式f′(x)≥x-2ax=(1-2a)x,从而可知当1-2a≥0,即a≤
时,f′(x)≥0判断出函数f(x)的单调性,得到答案.
(2)先证明ex≥1+x可得不等式f′(x)≥x-2ax=(1-2a)x,从而可知当1-2a≥0,即a≤
| 1 |
| 2 |
解答:
解:(1)当a=0时,f(x)=ex-1-x,
f′(x)=ex-1,
∵当x>0时,f′(x)>0,当x<0时,f′(x)<0,
∴f(x)在(-∞,0)上为减函数,在(0,+∞)上为增函数;
(2)令g(x)=ex-1-x,g′(x)=ex-1.
当x∈(-∞,0)时,g′(x)<0;当x∈(0,+∞)时,g'(x)>0.
故g(x)在(-∞,0)单调减少,在(0,+∞)单调增加.
∴g(x)≥g(0)=0,
∴ex≥1+x,当且仅当x=0时等号成立.
∵f′(x)=ex-1-2ax,
∴f′(x)≥x-2ax=(1-2a)x,
从而当1-2a≥0,即a≤
时,f′(x)≥0(x≥0),而f(0)=0,
于是当x≥0时,f(x)≥0.
由ex>1+x(x≠0)可得e-x>1-x(x≠0).
从而当a>
时,f′(x)<ex-1+2a(e-x-1)=e-x(ex-1)(ex-2a),
故当x∈(0,ln2a)时,f′(x)<0,而f(0)=0,于是当x∈(0,ln2a)时,f(x)<0.
综合得a的取值范围为(-∞,
].
f′(x)=ex-1,
∵当x>0时,f′(x)>0,当x<0时,f′(x)<0,
∴f(x)在(-∞,0)上为减函数,在(0,+∞)上为增函数;
(2)令g(x)=ex-1-x,g′(x)=ex-1.
当x∈(-∞,0)时,g′(x)<0;当x∈(0,+∞)时,g'(x)>0.
故g(x)在(-∞,0)单调减少,在(0,+∞)单调增加.
∴g(x)≥g(0)=0,
∴ex≥1+x,当且仅当x=0时等号成立.
∵f′(x)=ex-1-2ax,
∴f′(x)≥x-2ax=(1-2a)x,
从而当1-2a≥0,即a≤
| 1 |
| 2 |
于是当x≥0时,f(x)≥0.
由ex>1+x(x≠0)可得e-x>1-x(x≠0).
从而当a>
| 1 |
| 2 |
故当x∈(0,ln2a)时,f′(x)<0,而f(0)=0,于是当x∈(0,ln2a)时,f(x)<0.
综合得a的取值范围为(-∞,
| 1 |
| 2 |
点评:本题考查的知识点是利用导数研究函数的单调性,利用导数研究函数的极值,是导数的综合应用,运算量大,综合性性,转化困难,属于难题.

练习册系列答案
相关题目
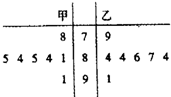 为迎接2013年全运会在注著名的海滨城市大连举行了场奥运选拔赛,其中甲乙两名运动员为争取最好一个参赛名额进行了7轮比赛的得分如茎叶图所示.
为迎接2013年全运会在注著名的海滨城市大连举行了场奥运选拔赛,其中甲乙两名运动员为争取最好一个参赛名额进行了7轮比赛的得分如茎叶图所示.