题目内容
设A={（x，y）|x+y＜3，x∈N，y∈N}，B={0，1，2}，f：（x，y）→x+y，这个对应是否为映射？是否为映射，是否是函数，说明原因．
考点：映射
专题：函数的性质及应用
分析：用列举法表示集合A，进而根据映射的定义可得A中任意一个元素，在B中都有唯一的元素与之对应，故这个对应是映射，但由于A集合不是数集，故这个对应不是函数．
解答：
解：∵A={（x，y）|x+y＜3，x∈N，y∈N}={（0，0），（0，1），（0，2），（1，0），（1，1），（2，0）}，
B={0，1，2}，f：（x，y）→x+y，
则A中任意一个元素，在B中都有唯一的元素与之对应，
故这个对应是映射，
但由于A集合不是数集，
故这个对应不是函数．
B={0，1，2}，f：（x，y）→x+y，
则A中任意一个元素，在B中都有唯一的元素与之对应，
故这个对应是映射，
但由于A集合不是数集，
故这个对应不是函数．
点评：本题考查的知识点是映射和函数的概念，熟练掌握映射和函数的定义是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=AA1=2，E是BC中点．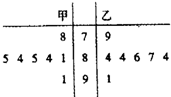
为迎接2013年全运会在注著名的海滨城市大连举行了场奥运选拔赛，其中甲乙两名运动员为争取最好一个参赛名额进行了7轮比赛的得分如茎叶图所示．