题目内容
数列{an}是等差数列,a1=f(x-1),a2=3,a3=f(x+1),其中f(x)=x2-4x+2(x≠0)
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)求数列{
}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)求数列{
| an |
| 2n |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由函数解析式结合a1=f(x-1),a3=f(x+1)求得a1,a3,由等差中项的概念列式求得x的值,则数列{an}的通项公式an可求;
(Ⅱ)把数列{an}的通项公式代入
,然后利用错位相减法求得数列{
}的前n项和Tn.
(Ⅱ)把数列{an}的通项公式代入
| an |
| 2n |
| an |
| 2n |
解答:
解:(Ⅰ)∵f(x)=x2-4x+2,
∴a1=f(x-1)=(x-1)2-4(x-1)+2=x2-6x+7,
a3=f(x+1)=(x+1)2-4(x+1)+2=x2-2x-1.
∵{an}是等差数列,
∴2a2=a1+a3,
即6=2x2-8x+6,
∴2x2-8x=0.
∵x≠0,
∴x=4.
当x=4时,a1=-1,a2=3,a3=7,
∴an=4n-5;
(Ⅱ)由题意,知Tn=
+
+
+…+
+
.
∴Tn=
+
+
+…+
+
①
Tn=
+
+
+ … +
+
②
①-②,得
Tn=-
+4(
+
+…+
)-
=-
+4×
-
=
-
,
∴Tn=3-
.
∴a1=f(x-1)=(x-1)2-4(x-1)+2=x2-6x+7,
a3=f(x+1)=(x+1)2-4(x+1)+2=x2-2x-1.
∵{an}是等差数列,
∴2a2=a1+a3,
即6=2x2-8x+6,
∴2x2-8x=0.
∵x≠0,
∴x=4.
当x=4时,a1=-1,a2=3,a3=7,
∴an=4n-5;
(Ⅱ)由题意,知Tn=
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| an-1 |
| 2n-1 |
| an |
| 2n |
∴Tn=
| -1 |
| 2 |
| 3 |
| 22 |
| 7 |
| 23 |
| 4n-9 |
| 2n-1 |
| 4n-5 |
| 2n |
| 1 |
| 2 |
| -1 |
| 22 |
| 3 |
| 23 |
| 7 |
| 24 |
| 4n-9 |
| 2n |
| 4n-5 |
| 2n+1 |
①-②,得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 4n-5 |
| 2n+1 |
=-
| 1 |
| 2 |
| ||||
1-
|
| 4n-5 |
| 2n+1 |
| 3 |
| 2 |
| 4n+3 |
| 2n+1 |
∴Tn=3-
| 4n+3 |
| 2n |
点评:本题考查了数列的函数特性,考查了等差数列的性质,训练了错位相减法求数列的和,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB折痕为AB′,AB′交DC于点P,当凹多边形ACB′PD的面积最大时制冷效果最好.
某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB折痕为AB′,AB′交DC于点P,当凹多边形ACB′PD的面积最大时制冷效果最好.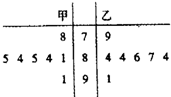 为迎接2013年全运会在注著名的海滨城市大连举行了场奥运选拔赛,其中甲乙两名运动员为争取最好一个参赛名额进行了7轮比赛的得分如茎叶图所示.
为迎接2013年全运会在注著名的海滨城市大连举行了场奥运选拔赛,其中甲乙两名运动员为争取最好一个参赛名额进行了7轮比赛的得分如茎叶图所示.