题目内容
观察下列等式；12=12，13+23=32，13+23+33=62，13+23+33+43=102，…根据上述规律，第n个等式为 ．
考点：归纳推理
专题：计算题,推理和证明
分析：根据题意，分析题干所给的等式可得：13+23=（1+2）2=32，13+23+33=（1+2+3）2 =62，13+23+33+43=（1+2+3+4）2 =102，进而可得答案．
解答：
解：根据题意，分析题干所给的等式可得：
13+23=（1+2）2=32，
13+23+33=（1+2+3）2 =62，
13+23+33+43=（1+2+3+4）2 =102，
则13+23+33+43+…+n3=（1+2+3+4+…+n）2 =（
）2，
故答案为：13+23+33+43+…+n3=（
）2
13+23=（1+2）2=32，
13+23+33=（1+2+3）2 =62，
13+23+33+43=（1+2+3+4）2 =102，
则13+23+33+43+…+n3=（1+2+3+4+…+n）2 =（
| n(n+1) |
| 2 |
故答案为：13+23+33+43+…+n3=（
| n(n+1) |
| 2 |
点评：本题考查归纳推理，解题的关键是发现各个等式之间变化的规律以及每个等式左右两边的关系．
练习册系列答案
相关题目
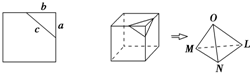在平面上，我们如果用一条直线去截正方形的一个角，那么截下的一个直角三角形，按图所标边长，由勾股定理有：c2=a2+b2．设想正方形换成正方体，把截线换成如图的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN，如果用S1，S2，S3表示三个侧面面积，S4表示截面面积，那么你类比得到的结论是