题目内容
已知函数f(x)满足:f2(x)-2f(x)f(x+1)+2f(x+1)=0(x∈R),
(1)用反证法证明:f(x)不可能为正比例函数;
(2)若f(0)=4,求f(1)、f(2)的值,并用数学归纳法证明:对任意的x∈N*,均有:2<f(x)<3.
(1)用反证法证明:f(x)不可能为正比例函数;
(2)若f(0)=4,求f(1)、f(2)的值,并用数学归纳法证明:对任意的x∈N*,均有:2<f(x)<3.
考点:数学归纳法,反证法与放缩法
专题:证明题,点列、递归数列与数学归纳法
分析:(1)运用反证法证明,假设f(x)=kx,(k≠0),代入条件化简整理,推出k=0与条件矛盾,得证;
(2)分别令x=0,x=1求出f(1),f(2),然后运用数学归纳法证明,注意x=k+1时的f(k+1)注意拆项和换元,运用对勾函数,求出范围即可得证.
(2)分别令x=0,x=1求出f(1),f(2),然后运用数学归纳法证明,注意x=k+1时的f(k+1)注意拆项和换元,运用对勾函数,求出范围即可得证.
解答:
(1)证明:假设f(x)=kx,(k≠0),
代入f2(x)-2f(x)f(x+1)+2f(x+1)=0(x∈R),
可得:-k2x2+(2k-2k2)x+2k=0对任意x恒成立,
故必有k=0,但由题设知k≠0,
故f(x)不可能为正比例函数.
(2)由f(0)=4,则f2(0)-2f(0)f(1)+2f(1)=0,
即16-8f(1)+2f(1)=0,可得:f(1)=
,
由f2(1)-2f(1)f(2)+2f(2)=0,可得f(2)=
.
证明:当x=1时:显然有2<f(1)<3成立.
假设当x=k时,仍然有2<f(k)<3成立.则当x=k+1时,
由原式整理可得:f(k+1)=
=
[(f(k)-1)+
+2].
令t=f(k)-1∈(1,2),故f(k+1)=
(t+
+2)∈(2,
)⊆(2,3).
故2<f(k+1)<3成立.
综上可得:对任意的x∈N*,均有2<f(x)<3.
代入f2(x)-2f(x)f(x+1)+2f(x+1)=0(x∈R),
可得:-k2x2+(2k-2k2)x+2k=0对任意x恒成立,
故必有k=0,但由题设知k≠0,
故f(x)不可能为正比例函数.
(2)由f(0)=4,则f2(0)-2f(0)f(1)+2f(1)=0,
即16-8f(1)+2f(1)=0,可得:f(1)=
| 8 |
| 3 |
由f2(1)-2f(1)f(2)+2f(2)=0,可得f(2)=
| 32 |
| 15 |
证明:当x=1时:显然有2<f(1)<3成立.
假设当x=k时,仍然有2<f(k)<3成立.则当x=k+1时,
由原式整理可得:f(k+1)=
| f2(k) |
| 2f(k)-2 |
| 1 |
| 2 |
| 1 |
| (f(k)-1) |
令t=f(k)-1∈(1,2),故f(k+1)=
| 1 |
| 2 |
| 1 |
| t |
| 9 |
| 4 |
故2<f(k+1)<3成立.
综上可得:对任意的x∈N*,均有2<f(x)<3.
点评:本题考查不等式的证明方法:反证法,数学归纳法,同时考查抽象函数的赋值法,考查基本的运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.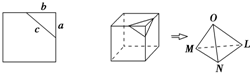 在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2.设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是
在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2.设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是