题目内容
14．函数y=f（x）的图象如图，则（ ）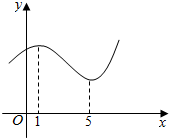
| A． | f′（3）＞3 | B． | f′（3）＜3 | C． | f′（3）=3 | D． | f′（3）的符号不确定 |
分析 由图象可知可知f（x）在（1，5）上单调递减，继而得到f′（x）＜0在（1，5）上恒成立，问题得以判断．
解答 解：由图象可知f（x）在（1，5）上单调递减，
∴f′（x）＜0在（1，5）上恒成立，
∴f′（3）＜0＜3，
故选：B．
点评 本题考查了导数和函数单调性的关系，以及函数图象的识别，属于基础题．
练习册系列答案
相关题目
4．几何体的三视图如图所示，则该几何体的体积为（ ）
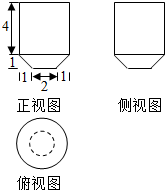
| A． | $\frac{53}{3}$π | B． | $\frac{55}{3}$π | C． | 18π | D． | $\frac{76}{3}$π |
5．表面积为40π的球面上有四点S、A、B、C且△SAB是等边三角形，球心O到平面SAB的距离为$\sqrt{2}$，若平面SAB⊥平面ABC，则三棱锥S-ABC体积的最大值为（ ）
| A． | 2 | B． | $\frac{2\sqrt{3}}{3}$ | C． | 6$\sqrt{6}$ | D． | $\frac{\sqrt{3}}{3}$ |
2．若椭圆$\frac{x^2}{4}+\frac{y^2}{m}=1$的离心率$e=\frac{{\sqrt{3}}}{2}$，则实数m的值是（ ）
| A． | 1 | B． | 1或16 | C． | $\frac{4}{3}$ | D． | 16 |
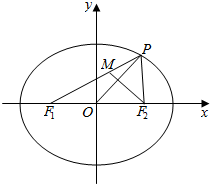如图，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点为F1、F2，P是椭圆上一点，M在PF1上，且满足$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$（λ∈R），PO⊥F2M，O为坐标原点．
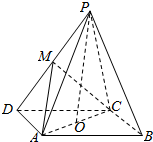如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC=1，PO⊥平面ABCD，O点在AC上，PO=2，M为PD中点．