题目内容

1．如图1，已知正方体ABCD-A1B1C1D1的棱长为a，动点M、N、Q分别在线段AD1、B1C、C1D1上，当三棱锥Q-BMN的正视图如图所示时，三棱锥Q-BMN的侧视图的面积等于（　　）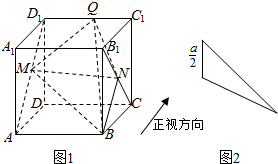
A．$\frac{1}{4}{a}^{2}$B．$\frac{3}{4}{a}^{2}$C．$\frac{1}{2}{a}^{2}$D．$\frac{\sqrt{3}}{2}{a}^{2}$

分析 由三棱锥Q-BMN的正视图可得Q在D1，N在C，所以三棱锥Q-BMN侧视图为△C1BC，即可求出三棱锥Q-BMN侧视图的面积．

解答 解：由三棱锥Q-BMN的正视图可得Q在D1，N在C，
所以三棱锥Q-BMN侧视图为△C1BC，
其面积为$\frac{1}{2}$•a•a=$\frac{1}{2}$a2，
故选：C．

点评 本题考查三棱锥Q-BMN正视图的面积，考查学生的计算能力，确定三棱锥Q-BMN侧视图为△C1BC是关键．

练习册系列答案
相关题目
11．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，过点（-2a，0）作椭圆的切线l．
（1）求切线l的斜率；
（2）平行移动直线l（移动过程中不过坐际原点），设移动后的直线与椭圆交于不同两点A，B，点B关于原点对称的点为C，若△ABC面积的最大值是2$\sqrt{3}$，求椭圆方程和平移后的直线方程．
12．已知定点A（4，0），P是椭圆4x2+9y2=36上的动点，则线段AP的中点的轨迹方程是4（x-2）2+9y2=9．
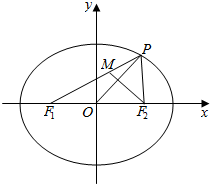9．如图，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点为F1、F2，P是椭圆上一点，M在PF1上，且满足$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$（λ∈R），PO⊥F2M，O为坐标原点．
（1）若椭圆方程为$\frac{x^2}{8}+\frac{y^2}{4}$=1，且P（2，$\sqrt{2}$），求点M的横坐标；
（2）若λ=2，求椭圆离心率e的取值范围．
16．若椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$和双曲线$\frac{x^2}{9}-\frac{y^2}{7}=1$有相同的焦点F1，F2，点P是两条曲线的一个交点，则PF1•PF2的值是16．
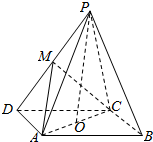6．如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC=1，PO⊥平面ABCD，O点在AC上，PO=2，M为PD中点．
（1）证明：AD⊥平面PAC；
（2）求三棱锥M-ACD的体积．
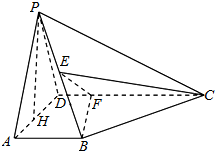13．如图所示，在四棱锥P-ABCD中，AB⊥平面PAD，AB∥CD，E是PB的中点，F是CD上的点，PH为△PAD中AD边上的高．
（Ⅰ）证明：PH⊥平面ABCD；
（Ⅱ）若PH=1，$AD=\sqrt{2}$，FC=1，求三棱锥E-BCF的体积．
10．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F（1，0），右顶点为M（$\sqrt{2}$，0）．
（1）求此椭圆的标准方程；
（2）设点P（2，0），点A是已知椭圆上的任意一点，点C是点A关于x轴的对称点，直线PA交椭圆于另一个不同的点B（不考虑直线PA的斜率为0的情形）．问：直线BC是否一定经过右焦点F？请说明理由．
11．设数列{an}的前n项和为Sn，其中an≠0，a1=1，且a1，Sn，an+1（n∈N*）成等差数列，则a2016=32014．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网