题目内容
15.函数f(x)=xsinx的导函数f′(x)在区间[-π,π]上的图象大致为( )| A. |  | B. | 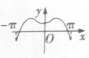 | C. | 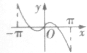 | D. | 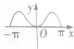 |
分析 求出函数f(x)的导数f′(x),结合函数的奇偶性,定义域,单调性的性质进行判断.
解答 解:函数的导数f′(x)=sinx+xcosx,
则f′(-x)=-sinx-xcosx=-(sinx+xcosx)=-f′(x),
则f′(x)为奇函数,图象关于原点对称,排除A,B,D,
故选:C
点评 本题主要考查函数导数的性质,以及函数图象的判断,求函数的导数,利用函数奇偶性的性质是解决本题的关键.

练习册系列答案
相关题目
5.表面积为40π的球面上有四点S、A、B、C且△SAB是等边三角形,球心O到平面SAB的距离为$\sqrt{2}$,若平面SAB⊥平面ABC,则三棱锥S-ABC体积的最大值为( )
| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | 6$\sqrt{6}$ | D. | $\frac{\sqrt{3}}{3}$ |
7.设F是椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的左焦点,P为椭圆上一点,M是PF的中点,且|PF|=4,则坐标原点O到点M的距离是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.直线3x-y=0绕原点逆时针旋转90°,再向右平移1个单位,所得到直线的方程为( )
| A. | x+3y-3=0 | B. | x+3y-1=0 | C. | 3x-y-3=0 | D. | x-3y+3=0 |
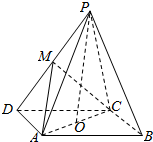 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,PO⊥平面ABCD,O点在AC上,PO=2,M为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,PO⊥平面ABCD,O点在AC上,PO=2,M为PD中点.