题目内容
 如图,O为坐标原点,点A,B在⊙O上,且点A在第一象限,点B(-
如图,O为坐标原点,点A,B在⊙O上,且点A在第一象限,点B(-| 3 |
| 5 |
| 4 |
| 5 |
(1)求sin2θ的值;
(2)若
| OA |
| OB |
| ||
| 2 |
考点:二倍角的正弦,平面向量数量积的运算,单位圆与周期性
专题:三角函数的求值,三角函数的图像与性质,平面向量及应用
分析:(1)由三角函数定义知cosθ=-
,sinθ=
,由二倍角公式可求sin2θ的值.
(2)先求cos∠BOA=
,可得∠BOA=45°,又∠BOC=θ,可得cos∠AOC=cos(∠BOC-∠BOA)=cos(θ-45°),可求cos(θ-45°)=
,从而可求点A的横坐标xA.
| 3 |
| 5 |
| 4 |
| 5 |
(2)先求cos∠BOA=
| ||
| 2 |
| ||
| 10 |
解答:
解:(1)因点C在 x轴正半轴上,点B(-
,
),∠COB=θ,
所以由三角函数定义知cosθ=-
,sinθ=
,…(3分)
所以sin2θ=2sinθcosθ=-
.…(6分)
(2)因为
•
=OA•OB•cos∠BOA=
,又OA=OB=
=1,
所以cos∠BOA=
,由题意可知∠BOA=45°,…(9分)
又∠BOC=θ,所以cos∠AOC=cos(∠BOC-∠BOA)=cos(θ-45°),
而cos(θ-45°)=cosθcos45°+sinθsin45°=
.…(12分)
故点A的横坐标xA=OA•cos∠AOC=1×
=
. …(14分)
| 3 |
| 5 |
| 4 |
| 5 |
所以由三角函数定义知cosθ=-
| 3 |
| 5 |
| 4 |
| 5 |
所以sin2θ=2sinθcosθ=-
| 24 |
| 25 |
(2)因为
| OA |
| OB |
| ||
| 2 |
(-
|
所以cos∠BOA=
| ||
| 2 |
又∠BOC=θ,所以cos∠AOC=cos(∠BOC-∠BOA)=cos(θ-45°),
而cos(θ-45°)=cosθcos45°+sinθsin45°=
| ||
| 10 |
故点A的横坐标xA=OA•cos∠AOC=1×
| ||
| 10 |
| ||
| 10 |
点评:本题主要考察了二倍角的正弦公式的应用,平面向量数量积的运算,单位圆与周期性,属于基本知识的考查.

练习册系列答案
相关题目
若x,y∈R且4x2+y2-2xy=2,则2x+y的最大值为( )
| A、2 | ||
B、
| ||
| C、4 | ||
D、2
|
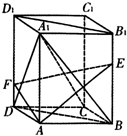 如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.
如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.