题目内容
已知f(x)=x2-2ax+2
(1)若f(x)在区间[2a-1,2a+1]为单调函数,求a的取值范围;
(2)求f(x)在[2,4]上的最小值.
(1)若f(x)在区间[2a-1,2a+1]为单调函数,求a的取值范围;
(2)求f(x)在[2,4]上的最小值.
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:(1)配方法化简f(x)=(x-a)2+2-a2,从而得到对称轴方程为x=a;从而求a;
(2)因为f(x)的对称轴方程为x=a,可按对称轴与区间的关系分三种情况讨论即可.
(2)因为f(x)的对称轴方程为x=a,可按对称轴与区间的关系分三种情况讨论即可.
解答:
 解:(1)f(x)=(x-a)2+2-a2,对称轴方程为x=a;
解:(1)f(x)=(x-a)2+2-a2,对称轴方程为x=a;
f(x)在区间[2a-1,2a+1]为单调函数,
∴a≤2a-1或a≥2a+1,
∴a≥1或a≤-1;
(2)因为f(x)的对称轴方程为x=a,可分以下三种情况:
①当a<2时,f(x)在[2,4]上为增函数,
所以f(x)min=f(2)=6-4a;
②当2≤a<4时,f(a)为最小值,
f(x)min=2-a2;
③当a≥4时,f(x)在[2,4]上为减函数,
所以f(x)min=f(4)=18-8a,
综上所述:f(x)min=
.
 解:(1)f(x)=(x-a)2+2-a2,对称轴方程为x=a;
解:(1)f(x)=(x-a)2+2-a2,对称轴方程为x=a;f(x)在区间[2a-1,2a+1]为单调函数,
∴a≤2a-1或a≥2a+1,
∴a≥1或a≤-1;
(2)因为f(x)的对称轴方程为x=a,可分以下三种情况:
①当a<2时,f(x)在[2,4]上为增函数,
所以f(x)min=f(2)=6-4a;
②当2≤a<4时,f(a)为最小值,
f(x)min=2-a2;
③当a≥4时,f(x)在[2,4]上为减函数,
所以f(x)min=f(4)=18-8a,
综上所述:f(x)min=
|
点评:本题考查了二次函数的性质应用,属于基础题.

练习册系列答案
相关题目
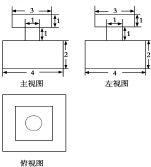
某品牌香水瓶的三视图如图(单位:cm),则该几何体的表面积为( )

A、(95-
| ||
B、(94-
| ||
C、(94+
| ||
D、(95+
|
空间几何体的三视图如图所示,则该几何体的表面积和体积分别为( )


A、6+2
| ||
B、8+2
| ||
C、8+2
| ||
D、6+2
|
 某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图2所示,已知130-140分数段的人数为80,90-100分数段的人数为a,则图1所示程序框图的运算结果为( )
某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图2所示,已知130-140分数段的人数为80,90-100分数段的人数为a,则图1所示程序框图的运算结果为( )| A、700! | B、710! |
| C、720! | D、730! |
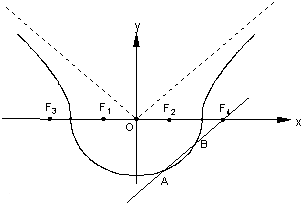 如图,曲线Γ由曲线
如图,曲线Γ由曲线