题目内容
若x≥0,y≥0,且x+2y=1,则2x+3y的最小值为( )
| A、2 | ||
B、
| ||
C、
| ||
| D、0 |
考点:基本不等式
专题:不等式的解法及应用
分析:由题意可得0≤y≤
,而2x+3y=2-y,由不等式的性质可得.
| 1 |
| 2 |
解答:
解:∵x≥0,y≥0,且x+2y=1,
∴2x+3y=2(1-2y)+3y=2-y,
∵x≥0,y≥0,∴1-2y≥0,解得0≤y≤
,
∴-
≤-y≤0,∴
≤2-y≤2,
∴2x+3y的最小值为
故选:B
∴2x+3y=2(1-2y)+3y=2-y,
∵x≥0,y≥0,∴1-2y≥0,解得0≤y≤
| 1 |
| 2 |
∴-
| 1 |
| 2 |
| 3 |
| 2 |
∴2x+3y的最小值为
| 3 |
| 2 |
故选:B
点评:本题考查不等式的性质,消元并求出y的精确范围是解决问题的关键,属基础题.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
设A,B是两个集合,有下列四个结论:
①若A?B,则对任意x∈A,有x∉B;
②若A?B,则集合A中的元素个数多于集合B中的元素个数;
③若A?B,则B?A;
④若A?B,则一定存在x∈A,有x∉B.
其中正确结论的个数为( )
①若A?B,则对任意x∈A,有x∉B;
②若A?B,则集合A中的元素个数多于集合B中的元素个数;
③若A?B,则B?A;
④若A?B,则一定存在x∈A,有x∉B.
其中正确结论的个数为( )
| A、4 | B、3 | C、2 | D、1 |
集合A={x|0<2x-1<3},B={x|-1<1og
x<0},则A∩(∁RB)=( )
| 1 |
| 2 |
| A、(0,1] |
| B、(1,2) |
| C、(-∞,0)∪(2,+∞) |
| D、∅ |
复数
在复平面内对应的点的坐标是( )
| 1+i |
| 1-i |
| A、(0,1) |
| B、(0,-1) |
| C、(1,0) |
| D、(-1,0) |
 随机地从甲乙两苗圃各抽取10株某种树苗,测量它们的株高(单位:cm),获得株高数据的茎叶图如图.
随机地从甲乙两苗圃各抽取10株某种树苗,测量它们的株高(单位:cm),获得株高数据的茎叶图如图.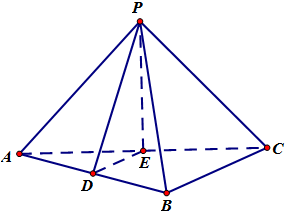 如图,在三棱锥P-ABC中,AB⊥BC,D,E分别是AB,AC的中点,且PE⊥平面ABC.求证:
如图,在三棱锥P-ABC中,AB⊥BC,D,E分别是AB,AC的中点,且PE⊥平面ABC.求证: