题目内容
函数f(x)=x2+2x+3,x∈[-1,1]的值域是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:根据函数解析式,求得函数对称轴和开口方向,判断函数在区间上的单调性,进而求得函数的最大和最小值,求得函数的值域.
解答:
解:函数f(x)的对称轴为x=-1,开口向上,
在区间[-1,1]但单调增,
∴f(x)max=f(1)=6,f(x)min=f(-1)=2,
∴函数的值域为[2,6].
故答案为:[2,6].
在区间[-1,1]但单调增,
∴f(x)max=f(1)=6,f(x)min=f(-1)=2,
∴函数的值域为[2,6].
故答案为:[2,6].
点评:本题主要考查了函数的值域问题,二次函数的性质.运用了数形结合思想解决问题较为直观.

练习册系列答案
相关题目
下列叙述错误的是( )
| A、频率是随机的,在试验前不能确定,随着试验次数的增加,频率一般会越来越接近概率 | ||
| B、互斥事件不一定是对立事件,但是对立事件一定是互斥事件 | ||
| C、若随机事件A发生的概率为p(A),则0≤p(A)≤1 | ||
D、某种彩票(有足够多)中奖概率为
|
函数f(x)=x3+x-1在(0,4)上零点的个数为( )
| A、0 | B、1 | C、2 | D、3 |
已知A(-2,-3),B(2,1),C(1,4),D(-7,-4),则有( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=2cos2x+6sinx+1的最大值为( )
| A、10 | B、9 | C、8 | D、7 |
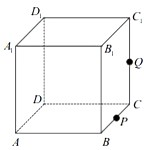 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是