题目内容
 一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球面面积的
一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球面面积的| 3 |
| 16 |
(1)试确定R与r的关系,并求出较大圆锥与较小圆锥的体积之比;
(2)求出两个圆锥的体积之和与球的体积之比.
考点:球的体积和表面积,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)设出球的半径,求出球的面积,然后求出圆锥的底面积,求出圆锥的底面半径,即可求出体积较小者的高与体积较大者的高的比值.
(2)由(1)分别求出两个圆锥体积的和及球的体积,可得答案.
(2)由(1)分别求出两个圆锥体积的和及球的体积,可得答案.
解答:
解:(1)不妨设球的半径为:4;
则球的表面积为:64π,圆锥的底面积为:12π,
∴圆锥的底面半径为:2
;
由几何体的特征知球心到圆锥底面的距离,球的半径以及圆锥底面的半径三者可以构成一个直角三角形
由此可以求得球心到圆锥底面的距离是
=2,
所以圆锥体积较小者的高为:4-2=2,
同理可得圆锥体积较大者的高为:4+2=6;
又由这两个圆锥的底面相同,
∴较大圆锥与较小圆锥的体积之比等于它们高之比,即3:1
(2)由(1)可得两个圆锥的体积和为:
•π•(2
)2•8=32π,
球的体积为:
•π•43=
π,
故两个圆锥的体积之和与球的体积之比为:32π:
π=3:8
则球的表面积为:64π,圆锥的底面积为:12π,
∴圆锥的底面半径为:2
| 3 |
由几何体的特征知球心到圆锥底面的距离,球的半径以及圆锥底面的半径三者可以构成一个直角三角形
由此可以求得球心到圆锥底面的距离是
42-(2
|
所以圆锥体积较小者的高为:4-2=2,
同理可得圆锥体积较大者的高为:4+2=6;
又由这两个圆锥的底面相同,
∴较大圆锥与较小圆锥的体积之比等于它们高之比,即3:1
(2)由(1)可得两个圆锥的体积和为:
| 1 |
| 3 |
| 3 |
球的体积为:
| 4 |
| 3 |
| 256 |
| 3 |
故两个圆锥的体积之和与球的体积之比为:32π:
| 256 |
| 3 |
点评:本题考查的知识点是球的体积和表面积,圆柱的体积和表面积,其中熟练掌握球和圆锥的体积表面积公式,是解答的关键.

练习册系列答案
相关题目
已知a∈R,则“a>2”是“a2>4”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
先把函数f(x)=sin(x-
)的图象上各点的横坐标变为原来的
倍(纵坐标不变),再把新得到的图象向右平移
个单位,得到y=g(x)的图象.当x∈(
,
))时,函数g(x)的值域为( )
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 4 |
| 3π |
| 4 |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
| D、[-1,0) |
若△ABC的内角A、B、C满足
=
=
,则cosB=( )
| 2 |
| sinA |
| 3 |
| sinB |
| 4 |
| sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
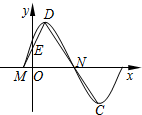 右图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
右图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<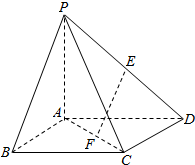 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且