题目内容
若△ABC的内角A、B、C满足
=
=
,则cosB=( )
| 2 |
| sinA |
| 3 |
| sinB |
| 4 |
| sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:正弦定理
专题:解三角形
分析:△ABC的内角A、B、C满足
=
=
,利用正弦定理
=
=
,可得a:b:c=2:3:4,再利用余弦定理即可得出.
| 2 |
| sinA |
| 3 |
| sinB |
| 4 |
| sinC |
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
解答:
解:∵△ABC的内角A、B、C满足
=
=
,由正弦定理可得
=
=
,
∴a:b:c=2:3:4,
设a=2k,b=3k,c=4k,(k>0).
由余弦定理可得:cosB=
=
=
.
故选:D.
| 2 |
| sinA |
| 3 |
| sinB |
| 4 |
| sinC |
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴a:b:c=2:3:4,
设a=2k,b=3k,c=4k,(k>0).
由余弦定理可得:cosB=
| a2+c2-b2 |
| 2ac |
| 4k2+16k2-9k2 |
| 2×2k×4k |
| 11 |
| 16 |
故选:D.
点评:本题考查了正弦定理与余弦定理,考查了计算能力,属于基础题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知数列{an}为等比数列,a5=1,a9=81,则a7=( )
| A、9或-9 | B、9 |
| C、27或-27 | D、-27 |
已知复数z1=-
+
i,z2=-
-
i,则下列命题中错误的是( )
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| A、z12=z2 |
| B、|z1|=|z2| |
| C、z13-z23=1 |
| D、zl、z2互为共轭复数 |
 一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球面面积的
一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球面面积的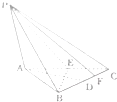 在三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,D,E分别为BC,AC的中点,F是CD的中点.
在三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,D,E分别为BC,AC的中点,F是CD的中点.