Question

6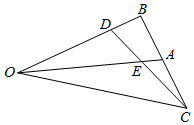．如图：已知，在△OBC中，点A是BC的中点，$\overrightarrow{OD}$=2$\overrightarrow{DB}$，DC和OA交于点E，则△OEC与△OBC的面积的比值是（　　）

• A． $\frac{4}{5}$
• B． $\frac{2}{5}$
• C． $\frac{3}{5}$
• D． $\frac{3}{8}$

Answer 1

分析 由条件即可得出$\overrightarrow{OA}=\frac{1}{2}（\overrightarrow{OB}+\overrightarrow{OC}）$，而O，E，A三点共线即可得到$\overrightarrow{OE}=λ\overrightarrow{OA}$，根据$\overrightarrow{OD}=2\overrightarrow{DB}$便可得到$\overrightarrow{OB}=\frac{3}{2}\overrightarrow{OD}$，这样即可得出$\overrightarrow{OE}=\frac{3λ}{4}\overrightarrow{OD}+\frac{λ}{2}\overrightarrow{OC}$，从而由C，E，D三点共线便可得出$\frac{3λ}{4}+\frac{λ}{2}=1$，可求出$λ=\frac{4}{5}$，这样由三角形的面积公式即可得出△OEC与△OBC的面积的比值．

解答 解：点A为BC的中点；
∴$\overrightarrow{OA}=\frac{1}{2}（\overrightarrow{OB}+\overrightarrow{OC}）$；
又O，E，A三点共线；
∴设$\overrightarrow{OE}=λ\overrightarrow{OA}=\frac{λ}{2}（\overrightarrow{OB}+\overrightarrow{OC}）$；
∵$\overrightarrow{OD}=2\overrightarrow{DB}$；
∴$\overrightarrow{OB}=\frac{3}{2}\overrightarrow{OD}$；
∴$\overrightarrow{OE}=\frac{3λ}{4}\overrightarrow{OD}+\frac{λ}{2}\overrightarrow{OC}$；
又C，E，D三点共线；
∴$\frac{3λ}{4}+\frac{λ}{2}=1$；
∴$λ=\frac{4}{5}$；
∴$\overrightarrow{OE}=\frac{4}{5}\overrightarrow{OA}$；
∴${S}_{△OEC}=\frac{4}{5}{S}_{△OAC}$=$\frac{4}{5}•\frac{1}{2}{S}_{△OBC}=\frac{2}{5}{S}_{△OBC}$．
故选B．

点评 考查向量加法的平行四边形法则，共线向量基本定理，向量的数乘运算，以及向量数乘的几何意义，三点A，B，C共线的充要条件：$\overrightarrow{OB}=λ\overrightarrow{OA}+μ\overrightarrow{OC}$，且λ+μ=1，以及三角形的面积公式，相似三角形对应边的比例关系．