题目内容
15.在△ABC中,角A,B,C的对边分别是a,b,c,且ccosA,bcosB,acosC成等差数列.(1)求角B的大小;
(2)若a+c=$\sqrt{10}$,b=2,求△ABC的面积.
分析 (1)由等差数列和正弦定理以及和差角的三角函数公式可得cosB,由三角形的内角的范围可得B=$\frac{π}{3}$;
(2)把已知数代入余弦定理整体可得ac=2,代入三角形的面积公式可得.
解答 解:(1)∵在△ABC中ccosA,bcosB,acosC成等差数列,
∴2bcosB=ccosA+acosC,
由正弦定理可得2sinBcosB=sinCcosA+sinAcosC,
∴2sinBcosB=sin(C+A)=sinB,由B∈(0,π)可得sinB>0,
约掉sinB可得cosB=$\frac{1}{2}$,再由B∈(0,π)可得B=$\frac{π}{3}$;
(2)∵a+c=$\sqrt{10}$,b=2,B=$\frac{π}{3}$,
∴由余弦定理可得b2=a2+c2-2accosB,
代入数据可得4=a2+c2-ac=(a+c)2-3ac=10-3ac,解得ac=2,
∴△ABC的面积S=$\frac{1}{2}$acsinB=$\frac{1}{2}$×2×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$
点评 本题考查正余弦定理解三角形,涉及整体思想和三角形的面积公式,属中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
5.已知函数f(x)=x|x-a|
(1)判断f(x)的奇偶性,并证明;
(2)求实数a的取值范围,使函数g(x)=f(x)+2x+1在R上恒为增函数;
(3)求函数f(x)在[-1,1]的最小值g(a).
(1)判断f(x)的奇偶性,并证明;
(2)求实数a的取值范围,使函数g(x)=f(x)+2x+1在R上恒为增函数;
(3)求函数f(x)在[-1,1]的最小值g(a).
6.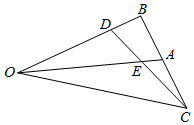 如图:已知,在△OBC中,点A是BC的中点,$\overrightarrow{OD}$=2$\overrightarrow{DB}$,DC和OA交于点E,则△OEC与△OBC的面积的比值是( )
如图:已知,在△OBC中,点A是BC的中点,$\overrightarrow{OD}$=2$\overrightarrow{DB}$,DC和OA交于点E,则△OEC与△OBC的面积的比值是( )
 如图:已知,在△OBC中,点A是BC的中点,$\overrightarrow{OD}$=2$\overrightarrow{DB}$,DC和OA交于点E,则△OEC与△OBC的面积的比值是( )
如图:已知,在△OBC中,点A是BC的中点,$\overrightarrow{OD}$=2$\overrightarrow{DB}$,DC和OA交于点E,则△OEC与△OBC的面积的比值是( )| A. | $\frac{4}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{8}$ |
7.已知集合A={-1,0,1},B={x|y=x2,x∈R},则A∩B=( )
| A. | {0,1} | B. | {-1,0,1} | C. | {1} | D. | ∅ |
4.如图所示的程序框图的运行结果为( )


| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |