题目内容
18.在等差数列{an}中,前m项(m为奇数)之和为98,其中奇数项之和为56,且am-a1=48.(1)求等差数列{an}的通项公式;
(2)求$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+$\frac{1}{{a}_{3}{a}_{4}}$+…$\frac{1}{{a}_{m-1}{a}_{m}}$的值.
分析 (1)由已知求得数列的偶数项的和,由奇数项和减去偶数项和求得中间项,再由前m项和求出m,结合am-a1=48求得公差,代入前m项和求得首项,则等差数列的通项公式可求;
(2)由$\frac{1}{{a}_{m-1}{a}_{m}}=\frac{1}{(8m-26)(8m-18)}$=$\frac{1}{8}(\frac{1}{8m-26}-\frac{1}{8m-18})$,利用裂项相消法求得$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+$\frac{1}{{a}_{3}{a}_{4}}$+…$\frac{1}{{a}_{m-1}{a}_{m}}$的值.
解答 解:(1)∵等差数列{an}的前m项(m为奇数)之和为98,其中奇数项之和为56,
∴其中偶数项的和为98-56=42,
∴中间项为56-42=14,
则14m=98,得m=7,
又am-a1=48,
∴a7-a1=6d=48,则d=8,
代入$7{a}_{1}+\frac{7×6×8}{2}=98$,得a1=-10.
∴an=-10+8(n-1)=8n-18;
(2)∵$\frac{1}{{a}_{m-1}{a}_{m}}=\frac{1}{(8m-26)(8m-18)}$=$\frac{1}{8}(\frac{1}{8m-26}-\frac{1}{8m-18})$,
∴$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+$\frac{1}{{a}_{3}{a}_{4}}$+…$\frac{1}{{a}_{m-1}{a}_{m}}$=$\frac{1}{8}(\frac{1}{-18}-\frac{1}{-10}+\frac{1}{-10}-\frac{1}{-2}+…+\frac{1}{8m-26}-\frac{1}{8m-18})$
=$\frac{1}{8}(-\frac{1}{18}-\frac{1}{8m-18})=\frac{m}{36(9-4m)}$.
点评 本题考查等差数列的通项公式,考查了等差数列的性质,训练了裂项相消法求数列的前n项和,是中档题.

| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
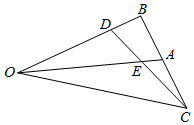 如图:已知,在△OBC中,点A是BC的中点,$\overrightarrow{OD}$=2$\overrightarrow{DB}$,DC和OA交于点E,则△OEC与△OBC的面积的比值是( )
如图:已知,在△OBC中,点A是BC的中点,$\overrightarrow{OD}$=2$\overrightarrow{DB}$,DC和OA交于点E,则△OEC与△OBC的面积的比值是( )| A. | $\frac{4}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{8}$ |
| A. | {0,1} | B. | {-1,0,1} | C. | {1} | D. | ∅ |
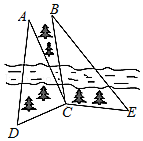 如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;
如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;