题目内容
16．在半径为1的圆周上任取两点，连成一条弦，求其长度超过该圆内接正三角形的边长的概率．分析 满足条件的事件对应的点在圆弧上它的长度是圆周的三分之一，根据几何概型公式得到概率．
解答 解：由题意知，试验发生包含的事件对应的点在圆周上，
因为圆的内接正三角形的边长确定为$\sqrt{3}$，
假设三角形的一个顶点A确定，那么另一点只能是B到C之间取出才能大于三角形的边长，
∴满足条件的事件对应的点在圆弧上它的长度是圆周的三分之一；
∴这样的事件发生的概率是$\frac{1}{3}$．
点评 本题考查几何概型，解题的关键是看出圆内接三角形的特点和圆内两点的连线之间的长度关系，属于基础题．
练习册系列答案
相关题目
6．
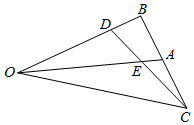如图：已知，在△OBC中，点A是BC的中点，$\overrightarrow{OD}$=2$\overrightarrow{DB}$，DC和OA交于点E，则△OEC与△OBC的面积的比值是（ ）
如图：已知，在△OBC中，点A是BC的中点，$\overrightarrow{OD}$=2$\overrightarrow{DB}$，DC和OA交于点E，则△OEC与△OBC的面积的比值是（ ）| A． | $\frac{4}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{3}{8}$ |
7．已知集合A={-1，0，1}，B={x|y=x2，x∈R}，则A∩B=（ ）
| A． | {0，1} | B． | {-1，0，1} | C． | {1} | D． | ∅ |
4．如图所示的程序框图的运行结果为（ ）
| A． | -1 | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
11．
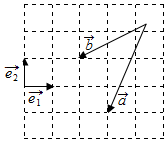如图，设$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$为互相垂直的单位向量，则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为（ ）
如图，设$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$为互相垂直的单位向量，则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为（ ）| A． | 2$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$ | B． | 3$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | C． | 2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$ | D． | $\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ |