题目内容
10.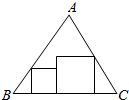 从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.
从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.
分析 设大小正方形的边长分别为x,y,(x,y>0).则$\frac{x}{\sqrt{3}}$+x+y+$\frac{y}{\sqrt{3}}$=3+$\sqrt{3}$,化为:x+y=3.利用x2+y2$≥\frac{(x+y)^{2}}{2}$即可得出.
解答 解:设大小正方形的边长分别为x,y,(x,y>0).
则$\frac{x}{\sqrt{3}}$+x+y+$\frac{y}{\sqrt{3}}$=3+$\sqrt{3}$,
化为:x+y=3.
则x2+y2$≥\frac{(x+y)^{2}}{2}$=$\frac{9}{2}$,当且仅当x=y=$\frac{3}{2}$时取等号.
∴这两个正方形的面积之和的最小值为$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查了正方形与等边三角形的性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.若△ABC的三边长分别为$\sqrt{3}$,2,$\sqrt{5}$,则△ABC的形状是( )
| A. | 一定是锐角三角形 | |
| B. | 一定是直角三角形 | |
| C. | 一定是钝角三角形 | |
| D. | 可能是锐角三角形,也可能是钝角三角形 |
2.已知定义在R上的函数f(x)满足f(-1+x)=f(3-x),当x≥1时,f(x)单调递增,则关于θ不等式$f(sin2θ)<f(log_8{2\sqrt{2}})$的解范围( )
| A. | $(kπ+\frac{π}{12},kπ+\frac{5π}{12}),k∈Z$ | B. | $(kπ+\frac{5π}{12},kπ+\frac{3π}{4}),k∈Z$ | ||
| C. | $(kπ-\frac{7π}{12},kπ+\frac{π}{12}),k∈Z$ | D. | $(kπ-\frac{5π}{12},kπ-\frac{π}{12}),k∈Z$ |
20.为了调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
(Ⅰ)完成以上2×2列联表,并估计该地区老年人中需要志愿者提供帮助的老年人的比例;
(Ⅱ)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
| 性别 是否需要志愿者 | 男 | 女 | 总计 |
| 需要 | 30 | ||
| 不需要 | 160 | ||
| 总计 | 200 | 500 |
(Ⅱ)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关.
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |