题目内容
18.已知函数f(x)是定义在R上的偶函数,且当x>0时,函数f(x)的解析式为$f(x)=\frac{2}{x}-1$.(1)求当x<0时函数f(x)的解析式;
(2)用定义证明f(x)在(0,+∞)上的是减函数.
分析 (1)当x<0时,-x>0,整体代入已知式子由偶函数可得;
(2)设x1,x2是(0,+∞)上任意两个实数,且x1<x2,作差判断f(x1)-f(x2)的符号可得.
解答 解:(1)当x<0时,-x>0,
∵当x>0时,函数f(x)的解析式为$f(x)=\frac{2}{x}-1$,
∴f(-x)=$\frac{2}{-x}$-1=-$\frac{2}{x}$-1,
由偶函数可知当x<0时,f(x)=f(-x)=-$\frac{2}{x}$-1;
(2)设x1,x2是(0,+∞)上任意两个实数,且x1<x2,
则f(x1)-f(x2)=$\frac{2}{{x}_{1}}$-1-$\frac{2}{{x}_{2}}$+1=$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}{x}_{2}}$,
由x1,x2的范围和大小关系可得f(x1)-f(x2)=$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}{x}_{2}}$>0,
∴f(x1)>f(x2),故f(x)在(0,+∞)上的是减函数
点评 本题考查函数解析的求解和定义法证明函数的单调性,属基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
8.已知向量$\overrightarrow a=(1,2)$,$\overrightarrow b=(-1,0)$,则$\overrightarrow a•\overrightarrow b$=( )
| A. | 3 | B. | 0 | C. | -1 | D. | 2 |
13.已知m是平面α的一条斜线,点A是平面α外的任意点,是经过点A的一条动直线,那么下列情形中可能出现的是( )
| A. | l∥m且l⊥平面α | B. | l⊥m且l∥平面α | C. | l⊥m且l⊥平面α | D. | l∥m且l∥平面α |
7.已知函数f(x)由下表给出,则f(2)=3.
| x | 1 | 2 | 3 |
| f(x) | 2 | 3 | 1 |
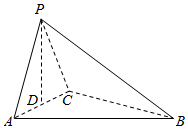 如图所示,在三棱锥P-ABC中,点P在平面ABC上的射影D与AC的中点重合,已知BC=2AC=8,AB=4$\sqrt{5}$.
如图所示,在三棱锥P-ABC中,点P在平面ABC上的射影D与AC的中点重合,已知BC=2AC=8,AB=4$\sqrt{5}$.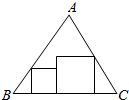 从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.
从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.