题目内容
5.若△ABC的三边长分别为$\sqrt{3}$,2,$\sqrt{5}$,则△ABC的形状是( )| A. | 一定是锐角三角形 | |
| B. | 一定是直角三角形 | |
| C. | 一定是钝角三角形 | |
| D. | 可能是锐角三角形,也可能是钝角三角形 |
分析 由余弦定理求得三角形的最大内角为锐角,可得△ABC的形状为锐角三角形.
解答 解:设最大边$\sqrt{5}$对应的角为θ,则θ为△ABC的最大内角,由余弦定理可得cosθ=$\frac{3+4-5}{2•2•\sqrt{3}}$=$\frac{\sqrt{3}}{6}$>0,
可得θ为锐角,故△ABC为锐角三角形,
故选:A.
点评 本题主要考查大边对大角,余弦定理的应用,属于基础题.

练习册系列答案
相关题目
13.已知m是平面α的一条斜线,点A是平面α外的任意点,是经过点A的一条动直线,那么下列情形中可能出现的是( )
| A. | l∥m且l⊥平面α | B. | l⊥m且l∥平面α | C. | l⊥m且l⊥平面α | D. | l∥m且l∥平面α |
17.为提高学生学习数学的兴趣,某地区举办了小学生“数独比赛”.比赛成绩共有90分,70分,60分,40分,30分五种,按本次比赛成绩共分五个等级.从参加比赛的学生中随机抽取了30名学生,并把他们的比赛成绩按这五个等级进行了统计,得到如下数据表:
(1)根据上面的统计数据,试估计从本地区参加“数独比赛”的小学生中任意抽取一人,其成绩等级为“A或B”的概率;
(2)从这30名学生中,随机选取2人,求“这两个人的成绩之差大于20分”的概率.
| 成绩等级 | A | B | C | D | E |
| 成绩(分) | 90 | 70 | 60 | 40 | 30 |
| 人数(名) | 4 | 6 | 10 | 7 | 3 |
(2)从这30名学生中,随机选取2人,求“这两个人的成绩之差大于20分”的概率.
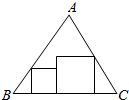 从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.
从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.