题目内容
20.为了调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:| 性别 是否需要志愿者 | 男 | 女 | 总计 |
| 需要 | 30 | ||
| 不需要 | 160 | ||
| 总计 | 200 | 500 |
(Ⅱ)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关.
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
分析 (Ⅰ)根据题意,计算表中缺少的数据,填写2×2列联表,
再根据表中数据计算需要帮助的老年人比例估计值;
(Ⅱ)根据表中数据,计算观测值,由此得出概率结论.
解答 解:(Ⅰ)根据题意,计算表中缺少的数据,填写2×2列联表如下:
| 性别 是否需要志愿者 | 男 | 女 | 总计 |
| 需要 | 40 | 30 | 70 |
| 不需要 | 160 | 270 | 430 |
| 总计 | 200 | 300 | 500 |
调查的500位老年人中,有70位需要志愿者提供帮助,因此该地区老年人中,
需要帮助的老年人的比例的估计值为$\frac{70}{500}$=14%. …(6分)
(Ⅱ)根据表中数据,计算观测值${k^2}=\frac{{500×{{(40×270-30×160)}^2}}}{70×430×200×300}≈9.967$,…(8分)
由于9.967>6.635,
所以有99%的把握认为该地区的老年人是否需要帮助与性别有关.…(10分)
点评 本题考查了2×2列联表以及独立性检验的应用问题,也考查了概率模型的应用问题,是基础题目.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
11. 某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
 某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )| A. | 20 | B. | 22.5 | C. | 22.75 | D. | 25 |
5.若x>0,则函数f(x)=4x+$\frac{2}{x}$的最小值是( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
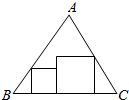 从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.
从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.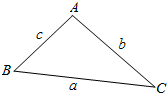 (1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.
(1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.