题目内容
已知函数sgn(x)=
,f(x)=x2•sgn[1+sgn(x)]+2x•sgn[1-sgn(x)],若函数g(x)=f(x)-m有两个零点,则m的取值范围是( )
|
| A、m<0 | B、0<m<1 |
| C、0<m≤1 | D、m>1 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:根据已知可得f(x)=
,若函数g(x)=f(x)-m有两个零点,则函数y=f(x)与y=m的图象有两个交点,画出函数f(x)的图象数形结合可得答案.
|
解答:
解:∵sgn(x)=
,
∴f(x)=x2•sgn[1+sgn(x)]+2x•sgn[1-sgn(x)]=
,
则函数f(x)的图象如下图所示:
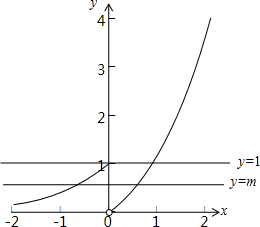
由图可知:
当0<m≤1时,函数g(x)=f(x)-m有两个零点,
故选:C
|
∴f(x)=x2•sgn[1+sgn(x)]+2x•sgn[1-sgn(x)]=
|
则函数f(x)的图象如下图所示:

由图可知:
当0<m≤1时,函数g(x)=f(x)-m有两个零点,
故选:C
点评:本题考查的知识点是根的存在性及根的个数判断,其中熟练掌握函数零点与方程根之间的对应关系是解答的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
已知f(x)=
,则f(-2)=( )
|
| A、-1 | B、3 | C、5 | D、1 |
设F1,F2是双曲线C的两焦点,点M在双曲线上,且∠MF2F1=
,若|F1F2|=8,|F2M|=
,则双曲线C的实轴长为( )
| π |
| 4 |
| 2 |
A、2
| ||
B、4
| ||
C、2
| ||
D、4
|
已知函数f(x)=
,则满足f(x)=
的x的值为( )
|
| 1 |
| 2 |
A、
| ||||
| B、-1 | ||||
C、
| ||||
D、
|
已知点(3,1)和(-1,5)在直线3x-2y+a=0的两侧,则a的取值范围是( )
| A、a<-7或 a>13 |
| B、-7<a<13 |
| C、a=7 或 a=13 |
| D、-13<a<7 |
已知双曲线
-
=1(a>0,b>0)的一个焦点与y2=20x的焦点重合,且双曲线的离心率为
,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2-
|
 如图,F1、F2是双曲线
如图,F1、F2是双曲线