题目内容
已知D是面积为1的△ABC的边AB上任一点，E是边AC上任一点，连结DE，F是线段DE上一点，连结BF，G是BF上一点，设
=λ1
，
=λ2
，
=λ3
，
=λ4
，且λ1+λ4-λ2-λ3=
，记△GDF的面积为S=f（λ1，λ2，λ3，λ4），则S的最大值是（ ）
| AD |
| AB |
| AE |
| AC |
| DF |
| DE |
| BG |
| BF |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：如图所示，连接AF，BE．由
=λ1
，
=λ2
，
=λ3
，
=λ4
，
利用三角形的面积计算公式可得
=
=1-λ4，
=
=1-λ1，
=
=λ3，
=
=λ2，由于S△ABC=1，λ1+λ4-λ2-λ3=
，
可得S=S△GDF=（1-λ4）（1-λ1）λ3λ2≤(
)4，即可得出．
| AD |
| AB |
| AE |
| AC |
| DF |
| DE |
| BG |
| BF |
利用三角形的面积计算公式可得
| S△GDF |
| S△BDF |
| BG |
| BF |
| S△BDF |
| S△ABF |
| BD |
| AB |
| S△ABF |
| S△ABE |
| DF |
| DE |
| S△ABE |
| S△ABC |
| AE |
| AC |
| 2 |
| 3 |
可得S=S△GDF=（1-λ4）（1-λ1）λ3λ2≤(
| 1-λ4+1-λ1+λ3+λ2 |
| 4 |
解答：
解：如图所示，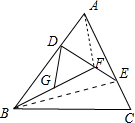
连接AF，BE．
∵
=λ1
，
=λ2
，
=λ3
，
=λ4
，
∴
=
=1-λ4，
=
=1-λ1，
=
=λ3，
=
=λ2，
又∵S△ABC=1，λ1+λ4-λ2-λ3=
，
∴S=S△GDF=（1-λ4）（1-λ1）λ3λ2≤(
)4=
．当且仅当1-λ4=1-λ1=λ3=λ2取等号．
∴S的最大值为
．
故选：D．
连接AF，BE．
∵
| AD |
| AB |
| AE |
| AC |
| DF |
| DE |
| BG |
| BF |
∴
| S△GDF |
| S△BDF |
| BG |
| BF |
| S△BDF |
| S△ABF |
| BD |
| AB |
| S△ABF |
| S△ABE |
| DF |
| DE |
| S△ABE |
| S△ABC |
| AE |
| AC |
又∵S△ABC=1，λ1+λ4-λ2-λ3=
| 2 |
| 3 |
∴S=S△GDF=（1-λ4）（1-λ1）λ3λ2≤(
| 1-λ4+1-λ1+λ3+λ2 |
| 4 |
| 1 |
| 81 |
∴S的最大值为
| 1 |
| 81 |
故选：D．
点评：本题考查了向量共线定理、三角形的面积计算公式、不等式的性质，考查了解决复杂问题的能力，属于难题．
练习册系列答案
相关题目
如图是一块带有圆形空洞和方形空洞的小木板，则下列物体中既可以堵住圆形空洞，又可以堵住方形空洞的是（ ）
已知几何体A-BCDE的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形，则该几何体的体积V的大小为
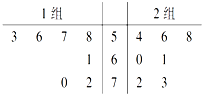如图是1，2两组各7名同学体重（单位：kg）数据的茎叶图．设1，2两组数据的平均数依次为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f（x）的图象是连续不断的，有如下x，f（x）对应值表：
其中a＜c＜0＜b，则函数f（x）在区间[1，6]上零点至少有（ ）
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f（x） | 10 | 13 | c | 7 | a | b |
| A、2个 | B、3个 | C、4个 | D、5个 |
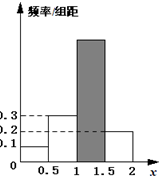如图所示的频率分布直方图，其中阴影部分的小长方形的高度是（ ）| A、0.4 | B、0.8 |
| C、1.4 | D、1.6 |
一个空间几何体的三视图及其相关数据如图所示，则这个空间几何体的表面积是（ ）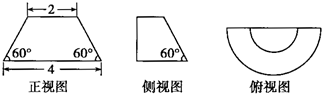
A、
| ||||
B、
| ||||
| C、11π | ||||
D、
|
若tanθ=2，则2sin2θ-sinθcosθ-cos2θ=（ ）
| A、5 | ||
| B、1 | ||
C、
| ||
D、
|