题目内容
19.在△ABC中,已知A=30°,a=2.(1)若C=105°,求边b的长;
(2)若△ABC为锐角三角形,求角B的取值范围;
(3)若△ABC为锐角三角形,求边b的长度的取值范围.
分析 (1)由题意可得B=45°,由正弦定理可得b=$\frac{asinB}{sinA}$,代值计算可得;
(2)由题意可得C=150°-B,由锐角三角形可得0°<B<90°且0°<150°-B<90°,解不等式组可得;
(3)由b=$\frac{asinB}{sinA}$=4sinB和(2)中求出的B的范围可得.
解答 解:(1)∵在△ABC中A=30°,a=2,C=105°,
∴B=180°-(A+C)=45°,
∴由正弦定理可得b=$\frac{asinB}{sinA}$=$\frac{2×\frac{\sqrt{2}}{2}}{\frac{1}{2}}$=2$\sqrt{2}$;
(2)∵A=30°,∴C=150°-B,
由锐角三角形可得0°<B<90°且0°<150°-B<90°,
解得60°<B<90°;
(3)由(2)可得60°<B<90°,
由正弦定理可得b=$\frac{asinB}{sinA}$=4sinB∈(2$\sqrt{3}$,4)
点评 本题考查正余弦定理解三角形,涉及锐角三角形的知识,属基础题.

练习册系列答案
相关题目
9.已知函数f(x)=x-alnx在区间(0,2]上单调递减,则实数a的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (0,2) | C. | ($\frac{1}{2}$,+∞) | D. | [2,+∞) |
10.某几何体的三视图如图,则该几何体的体积为( )
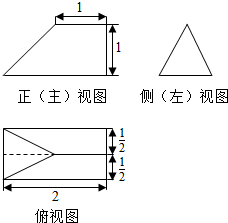

| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
11.棱长为1的正方体ABCD-A1B1C1D1中,$\overrightarrow{A{B_1}}•\overrightarrow{B{C_1}}$的值为( )
| A. | -1 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |