题目内容
18.已知数列{an}满足an+1=2n-3an,n∈N*(1)设bn=$\frac{{a}_{n}}{{2}_{n}}$,求数列{bn}的通项公式(用a1和n表示);
(2)求使得数列{an}单调递增的所有a1的值.
分析 (1)由an+1=2n-3an(n∈N*),得$\frac{{a}_{n+1}}{{2}^{n+1}}=\frac{1}{2}-\frac{3}{2}•\frac{{a}_{n}}{{2}^{n}}$,即${b}_{n+1}=-\frac{3}{2}{b}_{n}+\frac{1}{2}$,然后构造等比数列{bn$-\frac{1}{5}$},则其通项公式可求;
(2)由(1)知,$\frac{{a}_{n}}{{2}^{n}}=(\frac{{a}_{1}}{2}-\frac{1}{5})•(-\frac{3}{2})^{n-1}+\frac{1}{5}$,化简求得${a}_{n}=(\frac{{a}_{1}}{2}-\frac{1}{5})•(-\frac{3}{2})^{n-1}•{2}^{n}+\frac{1}{5}•{2}^{n}$,求出an-an-1,然后对${a}_{1}=\frac{2}{5}$,${a}_{1}<\frac{2}{5}$,${a}_{1}>\frac{2}{5}$讨论,可得使得数列{an}单调递增的a1的值为$\frac{2}{5}$.
解答 解:(1)∵an+1=2n-3an(n∈N*),
∴$\frac{{a}_{n+1}}{{2}^{n+1}}=\frac{1}{2}-\frac{3}{2}•\frac{{a}_{n}}{{2}^{n}}$,
又bn=$\frac{{a}_{n}}{{2}^{n}}$,∴${b}_{n+1}=\frac{1}{2}-\frac{3}{2}{b}_{n}$,即${b}_{n+1}=-\frac{3}{2}{b}_{n}+\frac{1}{2}$,
变形得,${b}_{n+1}-\frac{1}{5}=-\frac{3}{2}({b}_{n}-\frac{1}{5})$,
当${a}_{1}=\frac{2}{5}$时,数列{bn}的通项公式为${b}_{n}=\frac{1}{5}$;
当${a}_{1}≠\frac{2}{5}$时,${b}_{1}-\frac{1}{5}≠0$,
∴数列{bn$-\frac{1}{5}$}是以$\frac{{a}_{1}}{2}-\frac{1}{5}$为首项,以$-\frac{3}{2}$为公比的等比数列,
则${b}_{n}-\frac{1}{5}=(\frac{{a}_{1}}{2}-\frac{1}{5})•(-\frac{3}{2})^{n-1}$,
即${b}_{n}=(\frac{{a}_{1}}{2}-\frac{1}{5})•(-\frac{3}{2})^{n-1}+\frac{1}{5}$;
(2)由(1)知,$\frac{{a}_{n}}{{2}^{n}}=(\frac{{a}_{1}}{2}-\frac{1}{5})•(-\frac{3}{2})^{n-1}+\frac{1}{5}$,
则${a}_{n}=(\frac{{a}_{1}}{2}-\frac{1}{5})•(-\frac{3}{2})^{n-1}•{2}^{n}+\frac{1}{5}•{2}^{n}$,
∴${a}_{n}-{a}_{n-1}=(\frac{{a}_{1}}{2}-\frac{1}{5})•2•(-3)^{n-1}+\frac{{2}^{n}}{5}$$-(\frac{{a}_{1}}{2}-\frac{1}{5})•2•(-3)^{n-2}-\frac{{2}^{n-1}}{5}$
=$(\frac{4}{5}-2{a}_{1})•(-3)^{n-2}+\frac{{2}^{n-1}}{5}$.
当${a}_{1}=\frac{2}{5}$时,$(\frac{4}{5}-2{a}_{1})•(-3)^{n-2}+\frac{{2}^{n-1}}{5}$=$\frac{{2}^{n-1}}{5}$>0;
当${a}_{1}<\frac{2}{5}$时,$\frac{4}{5}-2{a}_{1}>0$,此时存在充分大的奇数,使得$(\frac{4}{5}-2{a}_{1})•(-3)^{n-2}+\frac{{2}^{n-1}}{5}$<0;
当${a}_{1}>\frac{2}{5}$时,$\frac{4}{5}-2{a}_{1}<0$,此时存在充分大的偶数,使得$(\frac{4}{5}-2{a}_{1})•(-3)^{n-2}+\frac{{2}^{n-1}}{5}$<0.
综上,使得数列{an}单调递增的a1的值为$\frac{2}{5}$.
点评 本题考查数列递推式,着重考查等比关系的确定及构造函数思想,考查推理、分析与运算的综合能力,属于难题.

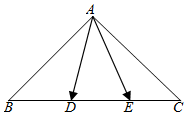 如图,在等腰直角三角形ABC中,AB=AC=$\sqrt{2}$,D,E是线段BC上的点,且DE=$\frac{1}{3}$BC,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是( )
如图,在等腰直角三角形ABC中,AB=AC=$\sqrt{2}$,D,E是线段BC上的点,且DE=$\frac{1}{3}$BC,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是( )| A. | $[{\frac{8}{9},\;\frac{4}{3}}]$ | B. | $[{\frac{4}{3},\;\frac{8}{3}}]$ | C. | $[{\frac{8}{9},\;\frac{8}{3}}]$ | D. | $[{\frac{4}{3},\;+∞})$ |
| A. | (0,$\frac{1}{2}$) | B. | (0,2) | C. | ($\frac{1}{2}$,+∞) | D. | [2,+∞) |
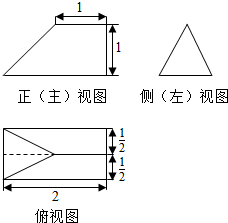
| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |