题目内容
定义:F(x,y)=yx(x>0,y>0),设数列{an}满足an=
,设Sn为数列{
}的前n项和,则Sn 1(填“>”、“=”、“<”).
| F(n,1) |
| F(2,n) |
| anan+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:由F(x,y)=yx(x>0,y>0),知an=
=
,故
=
=
=
-
,由此能求出结果.
| F(n,1) |
| F(2,n) |
| 1 |
| n2 |
| anan+1 |
|
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:∵F(x,y)=yx(x>0,y>0),
∴an=
=
,
∴
=
=
=
-
,
∴Sn=1-
+
-
+…+
-
=1-
<1.
故答案为:<.
∴an=
| F(n,1) |
| F(2,n) |
| 1 |
| n2 |
∴
| anan+1 |
|
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
故答案为:<.
点评:本题考查数列的递推式的应用,是基础题.解题时要认真审题,仔细解答,注意裂项求和法的合理运用.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知△ABC中,AB=6,∠A=30°,∠B=120°,则△ABC的面积为( )
| A、9 | ||
| B、18 | ||
C、9
| ||
D、18
|
若定义在R上的函数f(x)的导函数为f'(x),且满足f'(x)>f(x),则f(2011)与f(2009)e2的大小关系为( )
| A、f(2011)<f(2009)e2 |
| B、f(2011)=f(2009)e2 |
| C、f(2011)>f(2009)e2 |
| D、不能确定 |
集合A={x|y=
},B={y|y=x2-1},则∁RA∪B=( )
| x2-4 |
| A、(-2,+∞) |
| B、[-2,+∞) |
| C、(-1,+∞) |
| D、[-1,+∞) |
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
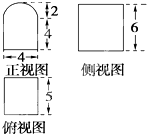

| A、92+24π |
| B、82+14π |
| C、92+14π |
| D、82+24π |
已知命题p:?x∈[1,2],x2-a≥0,命题q:?x∈R使x2+2ax+2-a=0,若命题“p且q”为真,则实数a的取值范围是( )
| A、{a|-1<a<1或a>1} |
| B、{a|a≥1} |
| C、{a|-2≤a≤1} |
| D、{a|a≤-2或a=1} |
