题目内容
已知函数f(x)=2-
(x>0),若存在实数m、n(m<n)使f(x)在区间(m,n)上的值域为(tm,tn),则实数t的取值范围是 .
| 1 |
| x |
考点:函数的值域
专题:函数的性质及应用
分析:结合函数的单调性,得出m,n是方程2-
=tx①的2个根,由题意得不等式组,解出即可.
| 1 |
| x |
解答:
解:画出函数f(x)的草图,如图示:
 ,
,
∴函数f(x)在(0,+∞)上单调递增,
∴2-
=tm,2-
=tn,
∴m,n是方程2-
=tx①的2个根,(0<m<n)
整理①得:tx2-2x+1=0,
∴
,解得:0<t<1,
故答案为:(0,1).
 ,
,∴函数f(x)在(0,+∞)上单调递增,
∴2-
| 1 |
| m |
| 1 |
| n |
∴m,n是方程2-
| 1 |
| x |
整理①得:tx2-2x+1=0,
∴
|
故答案为:(0,1).
点评:本题考查了函数的单调性,函数的定义域,值域问题,是一道中档题.

练习册系列答案
相关题目
若函数f(x)=
,则f(π)=( )
|
| A、0 | B、1 | C、0或1 | D、不确定 |
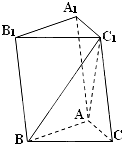 如图,斜三棱柱ABC-A1B1C1中,AB=3,AC=2,AB⊥AC,A1C1⊥BC1侧棱与底面成60°角.
如图,斜三棱柱ABC-A1B1C1中,AB=3,AC=2,AB⊥AC,A1C1⊥BC1侧棱与底面成60°角.