题目内容
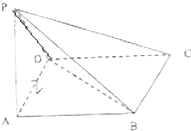 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=| 2 |
| 2 |
(1)求证:平面PAB⊥平面PCD
(2)在线段AB上是否存在点G,使得平面PCD与平面PGD夹角的余弦值为
| 1 |
| 3 |
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)先证明CD⊥PA,然后证明PA⊥PD.利用直线与平面垂直的判定定理证明PA⊥平面PCD,最后根据面面垂直的判定定理即可得到面PAB⊥面PDC.
(2)假设在线段AB上,存在点G,使得二面角C-PD-G的余弦值为
,然后以O为原点,直线OA,OF,OP分别为x,y,z轴建立空间直角坐标系,设G(1,a,0)(0≤a≤2).利用空间向量的坐标运算求出a值,即可得出结论.
(2)假设在线段AB上,存在点G,使得二面角C-PD-G的余弦值为
| 1 |
| 3 |
解答:
解:(1)∵平面PAD⊥平面ABCD,平面PAD∩面ABCD=AD
ABCD为正方形,CD⊥AD,CD?平面ABCD
∴CD⊥平面PAD.
∴CD⊥PA.
又∵AD=
PA=
PD.
∴PA=PD=
AD,
∴△PAD是等腰直角三角形,
且∠APD=90°,
即PA⊥PD
CD∩PD=D,且CD、PD?面PDC
∴PA⊥面PDC
又PA?面PAB,
∴面PAB⊥面PDC.
(2)如图,取AD的中点O,连结OP,OF.
∵PA=PD,∴PO⊥AD.
∵侧面PAD⊥底面ABCD,
面PAD⊥面ABCD,
∴PO⊥面ABCD,
而O,F分别为AD,BD的中点,∴OF∥AB,
又ABCD是正方形,故OF⊥AD.
∵PA=PD=
AD,∴PA⊥PD,OP=OA=1.
以O为原点,直线OA,OF,OP分别为x,y,z轴建立空间直角坐标系,
则有A(1,0,0),F(0,1,0),D(-1,0,0),P(0,0,1).
若在AB上存在点G,使得二面角C-PD-G的余弦值为
,
连结PG,DG
设G(1,a,0)(0≤a≤2).
由以上知平面PDC的法向量为
=(1,0,-1).
设平面PGD的法向量为
=(x,y,z).
∵
=(1,0,1),
=(-2,-a,0),
∴由
,
令x=1,则y=-
,z=-1,
故
=(1,-
,-1),
∴cos<
,
>=
=
,
解得a=
.
则在线段AB上存在点G(1,
,0),使得二面角C-PD-G的余弦值为
.
ABCD为正方形,CD⊥AD,CD?平面ABCD
∴CD⊥平面PAD.
∴CD⊥PA.
又∵AD=
| 2 |
| 2 |

∴PA=PD=
| ||
| 2 |
∴△PAD是等腰直角三角形,
且∠APD=90°,
即PA⊥PD
CD∩PD=D,且CD、PD?面PDC
∴PA⊥面PDC
又PA?面PAB,
∴面PAB⊥面PDC.
(2)如图,取AD的中点O,连结OP,OF.
∵PA=PD,∴PO⊥AD.
∵侧面PAD⊥底面ABCD,
面PAD⊥面ABCD,
∴PO⊥面ABCD,
而O,F分别为AD,BD的中点,∴OF∥AB,
又ABCD是正方形,故OF⊥AD.
∵PA=PD=
| ||
| 2 |
以O为原点,直线OA,OF,OP分别为x,y,z轴建立空间直角坐标系,
则有A(1,0,0),F(0,1,0),D(-1,0,0),P(0,0,1).
若在AB上存在点G,使得二面角C-PD-G的余弦值为
| 1 |
| 3 |
连结PG,DG
设G(1,a,0)(0≤a≤2).
由以上知平面PDC的法向量为
| PA |
设平面PGD的法向量为
| n |
∵
| DP |
| GD |
∴由
|
令x=1,则y=-
| 2 |
| a |
故
| n |
| 2 |
| a |
∴cos<
| n |
| PA |
| 2 | ||||||
|
| 1 |
| 3 |
解得a=
| 1 |
| 2 |
则在线段AB上存在点G(1,
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题考查直线与平面垂直的判定以及二面角的平面角及求法,考查逻辑推理能力.建立坐标系,利用向量法是解决本题的关键.

练习册系列答案
相关题目
过点(
,
)且被圆C:x2+y2-2x-4y=0截得的最短弦的弦长为( )
| 5 |
| 2 |
| 3 |
| 2 |
A、3
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=max{x2-x,1-x2}的单调增区间是( )
A、[-
| ||
B、(-∞,-
| ||
C、[-
| ||
| D、[0,1] |
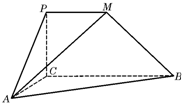 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.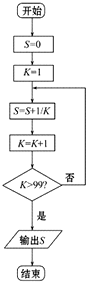 给出一个算法的程序框图(如图所示).
给出一个算法的程序框图(如图所示).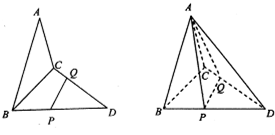 如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合. 如图所示,等边△ABC的边长为2,以A为圆心,半径为1作圆,PQ是圆的直径,求
如图所示,等边△ABC的边长为2,以A为圆心,半径为1作圆,PQ是圆的直径,求