题目内容
4.若函数f(x)=$(\frac{\sqrt{2}}{2})^{\sqrt{a{x}^{2}+2x+3}}$的最小值为$\frac{1}{2}$,则a=-1.分析 由指数函数y=$(\frac{\sqrt{2}}{2})^{x}$在R上是减函数知x≥2,从而化为y=$\sqrt{a{x}^{2}+2x+3}$的最小值为2,从而可得y=ax2+2x+3的最小值为4,从而求a.
解答 解:∵y=$(\frac{\sqrt{2}}{2})^{x}$在R上是减函数,
又∵$(\frac{\sqrt{2}}{2})^{x}$≤$\frac{1}{2}$;
∴x≥2,
故y=$\sqrt{a{x}^{2}+2x+3}$的最小值为2,
故y=ax2+2x+3的最小值为4,
而y=ax2+2x+3的图象的对称轴为x=-$\frac{1}{a}$,
故y=ax2+2x+3的最小值为3-$\frac{1}{a}$=4,
故a=-1;
故答案为:-1.
点评 本题考查了指数函数,幂函数,二次函数的性质的判断与应用,同时考查了复合函数的性质的应用.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
19.已知扇形的周长为10,扇形圆心角的弧度数是3,则扇形的面积为( )
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
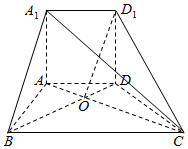 如图所示的一个几何体A1D1-ABCD中,底面ABCD为一个等腰梯形,AD∥BC且AD=$\sqrt{2}$,BC=2$\sqrt{2}$,对角线AC⊥BD,且交于点O,正方形ADD1A1垂直于底面ABCD.
如图所示的一个几何体A1D1-ABCD中,底面ABCD为一个等腰梯形,AD∥BC且AD=$\sqrt{2}$,BC=2$\sqrt{2}$,对角线AC⊥BD,且交于点O,正方形ADD1A1垂直于底面ABCD.