题目内容
15.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{{e}^{x}},x≤0}\\{1,0<x<e}\\{lnx,x≥e}\end{array}\right.$,则f(x)的最小值是1.分析 按分段函数分段讨论函数的取值,从而求函数的最小值.
解答 解:当x≤0时,f(x)=$\frac{1}{{e}^{x}}$≥1;
当0<x<e时,f(x)=1,
当x≥e时,f(x)=lnx≥lne=1;
故f(x)的最小值是1,
故答案为:1.
点评 本题考查了分段函数的应用及分类讨论的思想应用.

练习册系列答案
相关题目
6.在平行四边形ABCD中,$\overrightarrow{AC}$•$\overrightarrow{CB}$=0,AC=$\sqrt{2}$,BC=1,若将其沿AC折成直二面角D-AC-B,则AC与BD所成的角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
7.已知椭圆:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,上顶点为B,右焦点为F,过A、B、F作圆C,若圆心C的横纵坐标相等,则该椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
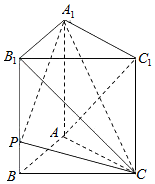 如图,已知直三棱柱ABC-A1B1C1中,AB⊥AC,AB=3,AC=4,B1C⊥AC1.
如图,已知直三棱柱ABC-A1B1C1中,AB⊥AC,AB=3,AC=4,B1C⊥AC1.