题目内容
求过圆O1:x2+y2-6x=0与圆O2:x2+y2=4的交点,分别满足下列条件的圆方程.
(1)过M(2,-2)的圆C1;
(2)圆心在直线x+y-1=0上的圆C2.
(1)过M(2,-2)的圆C1;
(2)圆心在直线x+y-1=0上的圆C2.
考点:圆的标准方程
专题:计算题,直线与圆
分析:设过圆O1:x2+y2-6x=0与圆O2:x2+y2=4的交点的方程为(x2+y2-6x)+λ(x2+y2-4)=0,
(1)M(2,-2)代入,求出λ,即可求出过M(2,-2)的圆C1;
(2)圆心代入直线x+y-1=0可得λ=-2,即可求出圆心在直线x+y-1=0上的圆C2.
(1)M(2,-2)代入,求出λ,即可求出过M(2,-2)的圆C1;
(2)圆心代入直线x+y-1=0可得λ=-2,即可求出圆心在直线x+y-1=0上的圆C2.
解答:
解:设过圆O1:x2+y2-6x=0与圆O2:x2+y2=4的交点的方程为(x2+y2-6x)+λ(x2+y2-4)=0,
(1)M(2,-2)代入可得(4+4-12)+λ(4+4-4)=0,∴λ=-3,
∴圆C1的方程为(x2+y2-6x)-3(x2+y2-4)=0,即x2+y2+3x-6=0;
(2)(x2+y2-6x)+λ(x2+y2-4)=0的圆心为(
,0),
代入直线x+y-1=0可得λ=-2,
∴圆心在直线x+y-1=0上的圆C2的方程为(x2+y2-6x)-2(x2+y2-4)=0,即x2+y2+6x-8=0.
(1)M(2,-2)代入可得(4+4-12)+λ(4+4-4)=0,∴λ=-3,
∴圆C1的方程为(x2+y2-6x)-3(x2+y2-4)=0,即x2+y2+3x-6=0;
(2)(x2+y2-6x)+λ(x2+y2-4)=0的圆心为(
| 3 |
| 1+λ |
代入直线x+y-1=0可得λ=-2,
∴圆心在直线x+y-1=0上的圆C2的方程为(x2+y2-6x)-2(x2+y2-4)=0,即x2+y2+6x-8=0.
点评:本题考查圆的方程,考查圆系方程,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
如图所示的程序框图输出的结果是S=14,则判断框内应填的条件是( )


| A、i≥7? | B、i>15? |
| C、i≥15? | D、i>31? |
如图,设全集U=R,M={x|x>2},N={0,1,2,3},则图中阴影部分所表示的集合是( )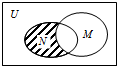

| A、{3} |
| B、{0,1} |
| C、{0,1,2} |
| D、{0,1,2,3} |