题目内容
某校有6间电脑室,每天晚上至少开放2间、则不同安排方案的种数为,①C62;②
+C63+2C64+C56+C66;③26-7;④P62,则正确的结论是( )
| C | 2 6 |
| A、仅有① | B、仅有② |
| C、有②和③ | D、仅有④ |
考点:组合及组合数公式
专题:排列组合
分析:由排列组合的知识易得,直接法,C62+C63+C64+C56+C66种,间接法,26-(C60+C61)=26-7种,可得答案.
解答:
解:6间电脑室至少开放2间即开放2间或3间或4间或5间或6间,
共有C62+C63+C64+C56+C66种方案,故②正确;
间接法,总的情况共26种,不合题意的有C60+C61种,
故共有26-(C60+C61)=26-7种方案,故③也正确,
故选:C
共有C62+C63+C64+C56+C66种方案,故②正确;
间接法,总的情况共26种,不合题意的有C60+C61种,
故共有26-(C60+C61)=26-7种方案,故③也正确,
故选:C
点评:本题考查简单的排列组合问题,属基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知平面α、β和直线m,l,则下列命题中正确的是( )
| A、若α⊥β,α∩β=m,l⊥m,则l⊥β |
| B、若α∩β=m,l?α,l⊥m,则l⊥β |
| C、若α⊥β,l?α,则l⊥β |
| D、若α⊥β,α∩β=m,l?α,l⊥m,则l⊥β |
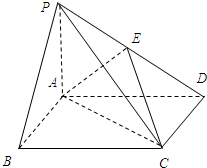 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.