题目内容
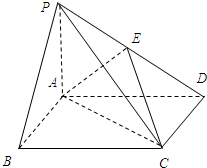 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.(1)求证:PB∥平面EAC;
(2)求证:平面PDC⊥平面PAD;
(3)求三棱锥P-ACE的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)连结AC,BD,交于点O,连结OE,由已知得OE∥PB,由此能证明PB∥平面EAC.
(2)由已知得PA⊥CD,AD⊥CD,得CD⊥平面PAD,由此能证明平面PDC⊥平面PAD.
(3)由三棱锥P-ACE的体积V=VP-ACD-VE-ACD,能求出结果.
(2)由已知得PA⊥CD,AD⊥CD,得CD⊥平面PAD,由此能证明平面PDC⊥平面PAD.
(3)由三棱锥P-ACE的体积V=VP-ACD-VE-ACD,能求出结果.
解答:
(1)证明: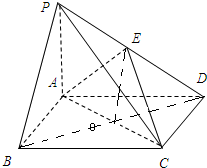 连结AC,BD,交于点O,
连结AC,BD,交于点O,
∵在底面ABCD是矩形,∴O是AC的中点,
连结OE,∵E是PD的中点,
∴OE∥PB,
∵OE?平面AEC,PB?AEC,
∴PB∥平面EAC.
(2)证明:∵在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,
∴PA⊥CD,AD⊥CD,
又PA∩AD=A,∴CD⊥平面PAD,
∵CD?平面PCD,
∴平面PDC⊥平面PAD.
(3)解:∵PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,
∴E到平面ACD的距离h=
PA=1,
S△ACD=
×4×2=4,
∴三棱锥P-ACE的体积V=VP-ACD-VE-ACD=
×4×4-
×2×4=
.
 连结AC,BD,交于点O,
连结AC,BD,交于点O,∵在底面ABCD是矩形,∴O是AC的中点,
连结OE,∵E是PD的中点,
∴OE∥PB,
∵OE?平面AEC,PB?AEC,
∴PB∥平面EAC.
(2)证明:∵在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,
∴PA⊥CD,AD⊥CD,
又PA∩AD=A,∴CD⊥平面PAD,
∵CD?平面PCD,
∴平面PDC⊥平面PAD.
(3)解:∵PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,
∴E到平面ACD的距离h=
| 1 |
| 2 |
S△ACD=
| 1 |
| 2 |
∴三棱锥P-ACE的体积V=VP-ACD-VE-ACD=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
点评:本题考查PB∥平面EAC的证明,考查平面PDC⊥平面PAD的证明,考查三棱锥P-ACE的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
设U=R,M={x|x2-x≤0},函数f(x)=
的定义域为N,则M∩(∁UN)=( )
| 1 | ||
|
| A、[0,1) | B、[0,1] |
| C、(0,1) | D、{1} |
某校有6间电脑室,每天晚上至少开放2间、则不同安排方案的种数为,①C62;②
+C63+2C64+C56+C66;③26-7;④P62,则正确的结论是( )
| C | 2 6 |
| A、仅有① | B、仅有② |
| C、有②和③ | D、仅有④ |