题目内容
二项式(x2-
)n展开式中的第三项与第五项的系数之比为-
,其中i为虚数单位,则展开式的常数项为( )
| i | ||
|
| 3 |
| 14 |
| A、72 | B、-72i |
| C、45 | D、-45i |
考点:二项式系数的性质
专题:二项式定理
分析:根据二项式(x2-
)n展开式中的第三项与第五项的系数之比为
=-
,求得得 n=10.在二项式(x2-
)10展开式的通项公式中,令x的幂指数等于零,求得r的值,可得展开式的常数项.
| i | ||
|
| ||
|
| 3 |
| 14 |
| i | ||
|
解答:
解:二项式(x2-
)n展开式中的第三项的系数为
•(-i)2,第五项的系数
•(-i)4,
∴二项式(x2-
)n展开式中的第三项与第五项的系数之比为
=
=-
,
解得n=10.
∴二项式(x2-
)10展开式的通项公式为Tr+1=
•(-i)r•x20-
.
令20-
=0,求得r=8,∴展开式的常数项为
•(-i)8=45,
故选:C.
| i | ||
|
| C | 2 n |
| C | 4 n |
∴二项式(x2-
| i | ||
|
| ||
|
| -12 |
| (n-2)(n-3) |
| 3 |
| 14 |
解得n=10.
∴二项式(x2-
| i | ||
|
| C | r 10 |
| 5r |
| 2 |
令20-
| 5r |
| 2 |
| C | 8 10 |
故选:C.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
(x2-x+1)10展开式中x3项的系数为( )
| A、-210 | B、210 |
| C、30 | D、-30 |
已知α是平面,m,n是直线,且m⊥α,则下列命题不正确的是( )
| A、若m∥n,则n⊥a |
| B、若n⊥α,则m∥n |
| C、若n∥α,则m⊥n |
| D、若m⊥n,则n∥α |
如果loga8>logb8>0,那么a、b间的关系是( )
| A、0<a<b<1 |
| B、1<a<b |
| C、0<b<a<1 |
| D、1<b<a |
已知a,b,c分别为△ABC内角A,B,C的对边,且a,b,c成等比数列,且B=
,则
+
=( )
| π |
| 3 |
| 1 |
| tanA |
| 1 |
| tanC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知三点A(2,1),B(1,-2),C(
,-
),动点P(a,b)满足0≤
•
≤2,且0≤
•
≤2,则动点P到点C的距离小于
的概率为( )
| 3 |
| 5 |
| 1 |
| 5 |
| OP |
| OA |
| OP |
| OB |
| 1 |
| 5 |
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
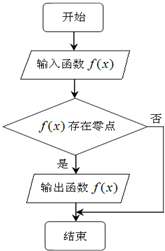 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|,则输出的函数的个数为( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|,则输出的函数的个数为( )