题目内容
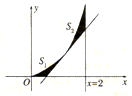 已知l1为函数f(x)=x2(x∈[0,2])在P(t,t2)(t∈(0,2))处的切线,l2为x=2,f(x),l1,l2与x轴所围成的图形如图所示.
已知l1为函数f(x)=x2(x∈[0,2])在P(t,t2)(t∈(0,2))处的切线,l2为x=2,f(x),l1,l2与x轴所围成的图形如图所示.(1)请用t表示S1+S2=g(t);
(2)求g(t)的最小值.
考点:定积分
专题:导数的概念及应用
分析:(1)先求根据导数求出切线方程,再根据微积分基本定理,问题得以解决.
(2)先求导,根据导数来求函数的最值.
(2)先求导,根据导数来求函数的最值.
解答:
解:(1)∵f(x)=x2,
∴f′(x)=2x,
∴l1为y-t2=2t(x-t),
即y=2tx-t2,它与x轴交于(
,0),与l2交于(2,4t-t2),
则g(t)=
x2-
(2-
)(4t-t2)
=-
+2t2-4t+
,(t∈(0,2));
(2)g′(′t)=-
+4t-4=-
(t-4)(t-
),
由g′(t)>0(0<t<2)得t∈(
,2),
∴g(x)在(
,2)上增,
由g′(t)<0,(0<t<2)得t∈(0,
),
∴g(x)在(0,
)上减,
∴gmin(x)=g(
)=
.
∴f′(x)=2x,
∴l1为y-t2=2t(x-t),
即y=2tx-t2,它与x轴交于(
| t |
| 2 |
则g(t)=
| ∫ | 2 0 |
| 1 |
| 2 |
| t |
| 2 |
=-
| t3 |
| 4 |
| 8 |
| 3 |
(2)g′(′t)=-
| 3t2 |
| 4 |
| 3 |
| 4 |
| 4 |
| 3 |
由g′(t)>0(0<t<2)得t∈(
| 4 |
| 3 |
∴g(x)在(
| 4 |
| 3 |
由g′(t)<0,(0<t<2)得t∈(0,
| 4 |
| 3 |
∴g(x)在(0,
| 4 |
| 3 |
∴gmin(x)=g(
| 4 |
| 3 |
| 8 |
| 27 |
点评:本题主要考查了微积分基本定理和定积分的几何意义.以及利用导数求函数的最值问题.

练习册系列答案
相关题目
 已知抛物线y2=2px(p>0)上的任意一点P到该抛物线焦点的距离比该点到y轴的距离多1.
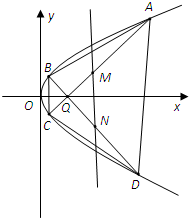
已知抛物线y2=2px(p>0)上的任意一点P到该抛物线焦点的距离比该点到y轴的距离多1.  如图,PC⊥平面ABC,DA∥PC,∠BCA=90°,AC=BC=1,PC=2,AD=1.
如图,PC⊥平面ABC,DA∥PC,∠BCA=90°,AC=BC=1,PC=2,AD=1.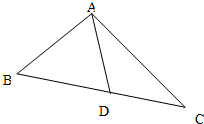 如图,在△ABC中,已知∠B=45°,D是BC边上的一点,AD=10,AC=14,DC=6.
如图,在△ABC中,已知∠B=45°,D是BC边上的一点,AD=10,AC=14,DC=6.