题目内容
已知正三角形ABC内接于半径为R的圆O.
(1)若在线段AB上任取一点D,求线段AD、DB的长都不小于
R的概率;
(2)若随机地向圆内丢一粒豆子,假设豆子落在圆内任一点是等可能的,求豆子落入正三角形ABC内的概率.
(1)若在线段AB上任取一点D,求线段AD、DB的长都不小于
| 1 |
| 2 |
(2)若随机地向圆内丢一粒豆子,假设豆子落在圆内任一点是等可能的,求豆子落入正三角形ABC内的概率.
考点:几何概型
专题:计算题,概率与统计
分析:(1)利用余弦定理求得AB长,求满足条件AD,BD不小于
R,D所在线段的长度,利用线段的长度比求概率;
(2)分别求得正三角形ABC的面积和其外接圆的面积,利用面积比求概率.
| 1 |
| 2 |
(2)分别求得正三角形ABC的面积和其外接圆的面积,利用面积比求概率.
解答:
解:(1)连接OA、OB,OA=OB=R,∠AOB=120°,∴AB=
=
R,
在AB上取P,Q,使AP=BQ=R,PQ=(
-1)R,
当在PQ上任取一点D,均使得AD,BD不小于
R,
∴在线段AB上任取一点D,线段AD、DB的长都不小于
R的概率为
=1-
;
(2)正三角形ABC的面积为
×
R×
R×
=
R2,
外接圆的面积为πR2,
∴随机地向圆内丢一粒豆子,豆子落入正三角形ABC内的概率为
.
R2+R2+2×
|
| 3 |
在AB上取P,Q,使AP=BQ=R,PQ=(
| 3 |
当在PQ上任取一点D,均使得AD,BD不小于
| 1 |
| 2 |
∴在线段AB上任取一点D,线段AD、DB的长都不小于
| 1 |
| 2 |
| ||
|
| ||
| 3 |
(2)正三角形ABC的面积为
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
3
| ||
| 4 |
外接圆的面积为πR2,
∴随机地向圆内丢一粒豆子,豆子落入正三角形ABC内的概率为
3
| ||
| 4π |
点评:本题考查了几何概型的概率计算,利用长度比、面积比、体积比求概率是几何概型求概率的常用方法.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
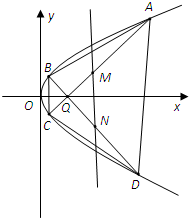 已知抛物线y2=2px(p>0)上的任意一点P到该抛物线焦点的距离比该点到y轴的距离多1.
已知抛物线y2=2px(p>0)上的任意一点P到该抛物线焦点的距离比该点到y轴的距离多1.