题目内容
给出四个等式:
1=1
1-4=-(1+2)
1-4+9=1+2+3
1-4+9-16=-(1+2+3+4)
…
(1)写出第5,6个等式,并猜测第n(n∈N*)个等式;
(2)用数学归纳法证明你猜测的等式.
1=1
1-4=-(1+2)
1-4+9=1+2+3
1-4+9-16=-(1+2+3+4)
…
(1)写出第5,6个等式,并猜测第n(n∈N*)个等式;
(2)用数学归纳法证明你猜测的等式.
考点:数学归纳法,归纳推理
专题:综合题,点列、递归数列与数学归纳法
分析:(1)本题考查归纳推理,解题时要认真分析题意中的等式,发现其变化的规律,注意验证即可;
(2)根据数学归纳法证明步骤即可证明.
(2)根据数学归纳法证明步骤即可证明.
解答:
解:(1)第5行 1-4+9-16+25=1+2+3+4+5-----------------------------------------(2分)
第6行 1-4+9-16+25-36=-(1+2+3+4+5+6)-------------------------------(4分)
第n行等式为:
12-22+32-42+…+(-1)n-1n2=(-1)n-1•(1+2+3+…+n).-------------(6分)
(2)证明:①当n=1时,左边=12=1,
右边=(-1)0×
=1,左边=右边,等式成立.--------------------(8分)
②假设n=k(k∈N*)时,等式成立,即12-22+32-42+…+(-1)k-1k2=(-1)k-1•
.
则当n=k+1时,
12-22+32-42+…+(-1)k-1k2+(-1)k(k+1)2
=(-1)k-1•
+(-1)k(k+1)2
=(-1)k(k+1)•[(k+1)-
]
=(-1)k•
.
∴当n=k+1时,等式也成立
根据①②可知,对于任何n∈N*等式均成立.--------------------------(12分)
第6行 1-4+9-16+25-36=-(1+2+3+4+5+6)-------------------------------(4分)
第n行等式为:
12-22+32-42+…+(-1)n-1n2=(-1)n-1•(1+2+3+…+n).-------------(6分)
(2)证明:①当n=1时,左边=12=1,
右边=(-1)0×
| 1×(1+1) |
| 2 |
②假设n=k(k∈N*)时,等式成立,即12-22+32-42+…+(-1)k-1k2=(-1)k-1•
| k(k+1) |
| 2 |
则当n=k+1时,
12-22+32-42+…+(-1)k-1k2+(-1)k(k+1)2
=(-1)k-1•
| k(k+1) |
| 2 |
=(-1)k(k+1)•[(k+1)-
| k |
| 2 |
=(-1)k•
| (k+1)[(k+1)+1] |
| 2 |
∴当n=k+1时,等式也成立
根据①②可知,对于任何n∈N*等式均成立.--------------------------(12分)
点评:用数学归纳法证明问题的步骤是:第一步验证当n=n0时命题成立,第二步假设当n=k时命题成立,那么再证明当n=k+1时命题也成立.本题解题的关键是利用第二步假设中结论证明当n=k+1时成立,本题是一个中档题目.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
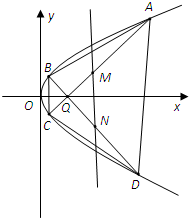 已知抛物线y2=2px(p>0)上的任意一点P到该抛物线焦点的距离比该点到y轴的距离多1.
已知抛物线y2=2px(p>0)上的任意一点P到该抛物线焦点的距离比该点到y轴的距离多1.  如图,PC⊥平面ABC,DA∥PC,∠BCA=90°,AC=BC=1,PC=2,AD=1.
如图,PC⊥平面ABC,DA∥PC,∠BCA=90°,AC=BC=1,PC=2,AD=1.