题目内容
18.已知两个单位向量$\overrightarrow a,\overrightarrow b$的夹角为60°,$\overrightarrow c=t\overrightarrow a+\overrightarrow b$,$\overrightarrow d=\overrightarrow a-t\overrightarrow b$,若$\overrightarrow c⊥\overrightarrow d$,则正实数t=1.分析 根据向量垂直得出$\overrightarrow{c}•\overrightarrow{d}=0$,列出方程解出t.
解答 解:$\overrightarrow{a}•\overrightarrow{b}=cos60°=\frac{1}{2}$.
∵$\overrightarrow{c}⊥\overrightarrow{d}$,
∴$\overrightarrow{c}•\overrightarrow{d}=0$,即(t$\overrightarrow{a}+\overrightarrow{b}$)($\overrightarrow{a}-t\overrightarrow{b}$)=0,
∴t${\overrightarrow{a}}^{2}$-t${\overrightarrow{b}}^{2}$+(1-t2)$\overrightarrow{a}•\overrightarrow{b}$=0,即-$\frac{1}{2}$t2+$\frac{1}{2}$=0.
∵t>0,
∴t=1.
故答案为1.
点评 本题考查了平面向量垂直与数量积的关系,数量积的运算,属于基础题.

练习册系列答案
相关题目
17.已知在数列{an}中,a1=$\frac{4}{5}$,an+1=$\left\{\begin{array}{l}{2{a}_{n},{a}_{n}∈[0,\frac{1}{2}]}\\{2{a}_{n}-1,{a}_{n}∈(\frac{1}{2},1]}\end{array}\right.$,则a2015等于( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
3.已知向量$\overrightarrow a=(-4,3)$,$\overrightarrow b=(5,6)$,则3|$\overrightarrow a{|^2}$$-4\overrightarrow a•\overrightarrow b$=( )
| A. | 83 | B. | 63 | C. | 57 | D. | 23 |
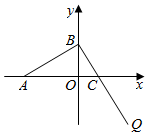 如图,已知A(-4a,0)(a>0),B、C两点分别在y轴和x轴上运动,并且满足$\overrightarrow{AB}$•$\overrightarrow{BQ}$=0,$\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{CQ}$.
如图,已知A(-4a,0)(a>0),B、C两点分别在y轴和x轴上运动,并且满足$\overrightarrow{AB}$•$\overrightarrow{BQ}$=0,$\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{CQ}$.