题目内容
6.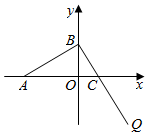 如图,已知A(-4a,0)(a>0),B、C两点分别在y轴和x轴上运动,并且满足$\overrightarrow{AB}$•$\overrightarrow{BQ}$=0,$\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{CQ}$.
如图,已知A(-4a,0)(a>0),B、C两点分别在y轴和x轴上运动,并且满足$\overrightarrow{AB}$•$\overrightarrow{BQ}$=0,$\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{CQ}$.(1)求动点Q的轨迹方程;
(2)设过点A的直线与点Q的轨迹交于E、F两点,A′(4a,0),求直线A′E、A′F的斜率之和.
分析 (1)分别设出Q、B、C的坐标,利用向量等式把B的坐标用Q的坐标表示,结合$\overrightarrow{AB}$•$\overrightarrow{BQ}$=0求得动点Q的轨迹方程;
(2)写出过点A的直线为y=k(x+4a)(k≠0),联立直线方程和抛物线方程,利用根与系数的关系得到E,F两点纵坐标的和,再写出直线A′E、A′F的斜率之和整理得答案.
解答 解:(1)设Q(x,y),B(0,yB),C(xC,0),
则$\overrightarrow{BC}=({x}_{C}-0,0-{y}_{B})$,$\overrightarrow{CQ}=(x-{x}_{C},y)$,
∵$\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{CQ}$,
∴$({x}_{C},-{y}_{B})=\frac{1}{3}(x-{x}_{C},y)$,则${y}_{B}=-\frac{y}{3}$,
又A(-4a,0)(a>0),
∴$\overrightarrow{AB}=(4a,-\frac{y}{3}),\overrightarrow{BQ}=(x,\frac{4y}{3})$,
由已知$\overrightarrow{AB}$•$\overrightarrow{BQ}$=0,则$4ax-\frac{4}{9}{y}^{2}=0$,
即y2=9ax,
∴动点Q的轨迹方程为y2=9ax;
(2)设过点A的直线为y=k(x+4a)(k≠0),
再设E(x1,y1),F(x2,y2),
联立$\left\{\begin{array}{l}{{y}^{2}=9ax}\\{y=k(x+4a)}\end{array}\right.$,得ky2-9ay+36a2k=0,
则${y}_{1}{y}_{2}=36{a}^{2}$,
∴kA′E+kA′F=$\frac{{y}_{1}}{{x}_{1}-4a}+\frac{{y}_{2}}{{x}_{2}-4a}=\frac{{y}_{1}{x}_{2}-4a{y}_{1}+{y}_{2}{x}_{1}-4a{y}_{2}}{({x}_{1}-4a)({x}_{2}-4a)}$
又${{y}_{1}}^{2}=9a{x}_{1},{{y}_{2}}^{2}=9a{x}_{2}$,
∴${k}_{A′E}+{k}_{A′F}=\frac{{y}_{1}\frac{{{y}_{2}}^{2}}{9a}-4a{y}_{1}+{y}_{2}\frac{{{y}_{1}}^{2}}{9a}-4a{y}_{2}}{({x}_{1}-4a)({x}_{2}-4a)}$=$\frac{({y}_{1}+{y}_{2})(\frac{{y}_{1}{y}_{2}}{9a}-4a)}{({x}_{1}-4a)({x}_{2}-4a)}$,
由${y}_{1}{y}_{2}=36{a}^{2}$,得kA′E+kA′F=0.
点评 本题考查平面向量的数量积运算,考查了轨迹方程的求法,训练了直线和圆锥曲线位置关系的应用,是中档题.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案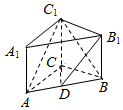 如图,已知侧棱垂直底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,点D是AB的中点.
如图,已知侧棱垂直底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,点D是AB的中点.