题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图所示,则φ=( )

| π |
| 2 |

A、-
| ||
B、
| ||
C、-
| ||
D、
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由函数图象的顶点求出A,由周期求出ω,由五点法作图求出φ的值.
解答:
解:有函数的图象顶点坐标可得A=2,再根据
T=
•
=
-
求得ω=2.
再根据五点法作图可得2×
+φ=
可得 φ=
,
故选:D.
| 1 |
| 4 |
| 1 |
| 4 |
| 2π |
| ω |
| π |
| 3 |
| π |
| 12 |
再根据五点法作图可得2×
| π |
| 12 |
| π |
| 2 |
| π |
| 3 |
故选:D.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数图象的顶点求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
相关题目
关于x的不等式x2-ax+a>0(a∈R)在R上恒成立的充分不必要条件是( )
| A、a<0或a>4 |
| B、0<a<2 |
| C、0<a<4 |
| D、0<a<8 |
已知△ABC是边长为4的等边三角形,点D、E分别满足
=-
、
=
,则
•
=( )
| DC |
| AC |
| BE |
| EC |
| AB |
| DE |
| A、8 | B、4 | C、-8 | D、-4 |
正方体ABCD-A1B1C1D1的棱长为a,M为AC1的中点,N为BB1的中点,则|MN|为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2a |
已知等比数列{an}的前3项分别为4、6、x,则x为 ( )
| A、7 | B、8 | C、9 | D、10 |
已知平面向量
=(0,1),
=(2,1),|λ
+
|=2,则λ=( )
| a |
| b |
| a |
| b |
A、1+
| ||
B、
| ||
| C、2 | ||
| D、-1 |
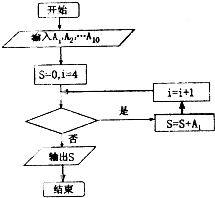 如表是我市抽查部分高中学生的身高统计表,从左到右的各组表示的学生人数依次记为A1,A2,…,A10(如A2表示身高[150,155)内的人数),如图是统计表中身高在一定范围内的学生人数的程序框图,如果要统计身高在160-180cm(含160cm不含180cm)的学生人数,那么空白的判断框内应填写的条件是( )
如表是我市抽查部分高中学生的身高统计表,从左到右的各组表示的学生人数依次记为A1,A2,…,A10(如A2表示身高[150,155)内的人数),如图是统计表中身高在一定范围内的学生人数的程序框图,如果要统计身高在160-180cm(含160cm不含180cm)的学生人数,那么空白的判断框内应填写的条件是( )