题目内容
已知函数f(x)=x-
(a∈R).
(1)当a=1时,证明:当x≥0时,f(x)≥0;
(2)当a=-1,证明:(1-
)f(x)>1-
.
| x2+ax |
| ex |
(1)当a=1时,证明:当x≥0时,f(x)≥0;
(2)当a=-1,证明:(1-
| lnx |
| x |
| 1 |
| e2 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)a=1时,令g(x)=ex-x-1,g'(x)=ex-1≥0,g(x)≥0,由此能证明当x≥0时,f(x)≥0.
(2)a=-1时,(1-
)f(x)=(x-lnx)(1-
),令h(x)=x-lnx,h′(x)=
,由此能证明(1-
)f(x)>1-
.
(2)a=-1时,(1-
| lnx |
| x |
| x-1 |
| ex |
| x-1 |
| x |
| lnx |
| x |
| 1 |
| e2 |
解答:
证明:(1)a=1时,f(x)=x-
=
(ex-x-1),
令g(x)=ex-x-1,g'(x)=ex-1≥0,
∴g(x)在[0,+∞)上为增函数…(3分)
g(x)≥g(0)=0,
∴当x≥0时,f(x)=
g(x)≥0.…(6分)
(2)a=-1时,(1-
)f(x)=(x-lnx)(1-
),
令h(x)=x-lnx,h′(x)=
,
0<x<1时,h'(x)<0,x>1时,h'(x)>0
∴h(x)在(0,1)上为减函数,在(1,+∞)上为增函数,…(9分)
∴h(x)≥h(1)①
令φ(x)=1-
,ϕ′(x)=
,
∴0<x<2时,φ'(x)<0,
x>2时,φ'(x)>0,
即φ(x)在(0,2)上为减函数,在(2,+∞)上为增函数
∴ϕ(x)≥ϕ(2)=1-
②,
∴由①②得(1-
)f(x)=h(x)φ(x)>1-
.…(12分)
| x2+x |
| ex |
| x |
| ex |
令g(x)=ex-x-1,g'(x)=ex-1≥0,
∴g(x)在[0,+∞)上为增函数…(3分)
g(x)≥g(0)=0,
∴当x≥0时,f(x)=
| x |
| ex |
(2)a=-1时,(1-
| lnx |
| x |
| x-1 |
| ex |
令h(x)=x-lnx,h′(x)=
| x-1 |
| x |
0<x<1时,h'(x)<0,x>1时,h'(x)>0
∴h(x)在(0,1)上为减函数,在(1,+∞)上为增函数,…(9分)
∴h(x)≥h(1)①
令φ(x)=1-
| x-1 |
| ex |
| x-2 |
| ex |
∴0<x<2时,φ'(x)<0,
x>2时,φ'(x)>0,
即φ(x)在(0,2)上为减函数,在(2,+∞)上为增函数
∴ϕ(x)≥ϕ(2)=1-
| 1 |
| e2 |
∴由①②得(1-
| lnx |
| x |
| 1 |
| e2 |
点评:本题考查不等式的证明,解题时要认真审题,合理构造函数,注意导数性质的合理运用.

练习册系列答案
相关题目
已知平面向量
=(0,1),
=(2,1),|λ
+
|=2,则λ=( )
| a |
| b |
| a |
| b |
A、1+
| ||
B、
| ||
| C、2 | ||
| D、-1 |
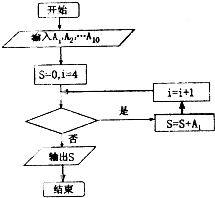 如表是我市抽查部分高中学生的身高统计表,从左到右的各组表示的学生人数依次记为A1,A2,…,A10(如A2表示身高[150,155)内的人数),如图是统计表中身高在一定范围内的学生人数的程序框图,如果要统计身高在160-180cm(含160cm不含180cm)的学生人数,那么空白的判断框内应填写的条件是( )
如表是我市抽查部分高中学生的身高统计表,从左到右的各组表示的学生人数依次记为A1,A2,…,A10(如A2表示身高[150,155)内的人数),如图是统计表中身高在一定范围内的学生人数的程序框图,如果要统计身高在160-180cm(含160cm不含180cm)的学生人数,那么空白的判断框内应填写的条件是( ) 已知正方形ABCD的边长为4,E,F分别是AB,AD的中点,GC⊥平面ABCD,GC=2,求三棱锥B-EFG的高.
已知正方形ABCD的边长为4,E,F分别是AB,AD的中点,GC⊥平面ABCD,GC=2,求三棱锥B-EFG的高.