题目内容
2.给出下列等式:①arcsin$\frac{π}{2}$=1;②arcsin(-$\frac{1}{2}$)=-$\frac{π}{6}$;③arcsinsin$\frac{π}{3}$=$\frac{π}{3}$;④sin(arcsin$\frac{1}{2}$)=$\frac{1}{2}$.其中正确等式的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据反正弦函数的定义域以及反正弦函数与正弦函数是互为反函数,对选项中的等式进行判定即可.
解答 解:①$\frac{π}{2}$>1,且arcsin1=$\frac{π}{2}$,∴①不正确;
②arcsin(-$\frac{1}{2}$)=-arcsin$\frac{1}{2}$=-$\frac{π}{6}$,∴②正确;
③arcsinsin$\frac{π}{3}$=arcsin$\frac{\sqrt{3}}{2}$=$\frac{π}{3}$,∴③正确;
④sin(arcsin$\frac{1}{2}$)=sin$\frac{π}{6}$=$\frac{1}{2}$,∴④正确;
综上,正确等式的个数是3.
故选:C.
点评 本题考查了反三角函数的定义域以及反正弦函数与正弦函数的运算问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.(2x-$\frac{1}{\sqrt{x}}$)12(x>0)的展开式中,第9项为( )
| A. | C${\;}_{12}^{8}$ | B. | C${\;}_{12}^{8}$24 | C. | -C${\;}_{12}^{9}$ | D. | -C${\;}_{12}^{9}$23 |
10.已知等比数列{an}的公比为q=-$\frac{1}{2}$.
(1)若a4=$\frac{1}{8}$,求数列{an}的前n项和;
(2)证明:对任意k∈N*,ak+2是ak与ak+1的等差中项.
(1)若a4=$\frac{1}{8}$,求数列{an}的前n项和;
(2)证明:对任意k∈N*,ak+2是ak与ak+1的等差中项.
17.设函数y=log2$\frac{3}{x-1}$的定义域为集合A,函数y=$\root{3}{x-2}$的定义域为集合B,则A∩B为( )
| A. | {x|x≥2} | B. | {x|x≠1} | C. | {x|x>2} | D. | {x|x>1} |
9.如图,在平面四边形ABCD中,AB=1,$BC=\sqrt{3}+1$,$AD=\sqrt{6}$,∠ABC=120°,∠DAB=75°,则CD=( )
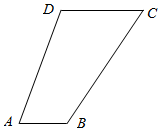

| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{2}+1$ |
 (文科)四棱镜P-ABCD中,PD⊥平面ABCD,2AD=AB=BC=2a,AD∥BC,PD=$\sqrt{3}$a,∠DAB=60°,Q是PB的中点.
(文科)四棱镜P-ABCD中,PD⊥平面ABCD,2AD=AB=BC=2a,AD∥BC,PD=$\sqrt{3}$a,∠DAB=60°,Q是PB的中点.