题目内容
6. (文科)四棱镜P-ABCD中,PD⊥平面ABCD,2AD=AB=BC=2a,AD∥BC,PD=$\sqrt{3}$a,∠DAB=60°,Q是PB的中点.
(文科)四棱镜P-ABCD中,PD⊥平面ABCD,2AD=AB=BC=2a,AD∥BC,PD=$\sqrt{3}$a,∠DAB=60°,Q是PB的中点.(Ⅰ)若平面PAD∩平面PBC=l,求证:l∥BC;
(Ⅱ)求证:DQ⊥PC.
分析 (Ⅰ)由AD∥BC,得BC∥平面PAD,由此能证明l∥BC.
(Ⅱ)连结BD,由余弦定理,得BD=$\sqrt{3}a$,从而BD⊥AD,BC⊥PD,进而BC⊥平面PBD,平面PBD⊥平面PBC,再由DQ⊥PB,得DQ⊥平面PBC,由此能证明DQ⊥PC.
解答 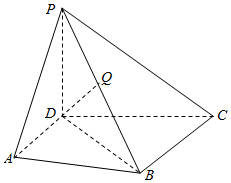 证明:(Ⅰ)∵AD∥BC,AD?平面PAD,BC?平面PAD
证明:(Ⅰ)∵AD∥BC,AD?平面PAD,BC?平面PAD
∴BC∥平面PAD,
又平面PBC过BC,且与平面PAD交于l,
∴l∥BC.
(Ⅱ)连结BD,△ABD中,AD=a,AB=2a,∠DAB=60°,
由余弦定理,得:
BD2=DA2+AB2-2DA•ABcos60°,
解得BD=$\sqrt{3}a$,
∵AB2=AD2+BD2,∴△ABD为直角三角形,BD⊥AD,
∵AD∥BC,∴BC⊥PD,
∵PD∩BD=D,∴BC⊥平面PBD,
∵BC?平面PBC,∴平面PBD⊥平面PBC,
又∵PD=BD=$\sqrt{3}a$,Q为PB中点,∴DQ⊥PB,
∵平面PBD∩平面PBC=PB,∴DQ⊥平面PBC,
∵PC?平面PBC,
∴DQ⊥PC.
点评 本题考查线面平行的证明,考查线线垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
1.若a=ln2,b=5${\;}^{-\frac{1}{2}}$,c=${∫}_{0}^{1}$xdx,则a,b,c的大小关系( )
| A. | a<b<cB | B. | b<a<cC | C. | b<c<a | D. | c<b<a |
11.已知向量$\overrightarrow{m}$=(1,cosθ),$\overrightarrow{n}$=(sinθ,-2),且$\overrightarrow{m}$⊥$\overrightarrow{n}$,则sin2θ+6cos2θ的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | -2 |
15.设等比数列{an}的前n项和为Sn,下列结论一定成立的是( )
| A. | a1+a3≥2a2 | B. | a1+a3≤2a2 | C. | a1S3>0 | D. | a1S3<0 |