题目内容
9.如图,在平面四边形ABCD中,AB=1,$BC=\sqrt{3}+1$,$AD=\sqrt{6}$,∠ABC=120°,∠DAB=75°,则CD=( )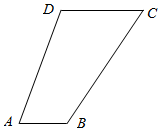
| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{2}+1$ |
分析 分别过C,D作AB的垂线DE,CF,则通过计算可得四边形DEFC为矩形,于是CD=EF=AB-AE+BF.
解答 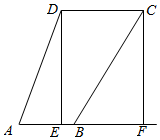 解过D作DE⊥AB于E,过C作CF⊥AB交AB延长线于F,
解过D作DE⊥AB于E,过C作CF⊥AB交AB延长线于F,
则DE∥CF,∠CBF=60°.
DE=ADsinA=$\sqrt{6}×\frac{\sqrt{6}+\sqrt{2}}{4}$=$\frac{3+\sqrt{3}}{2}$,CF=BCsin∠CBF=($\sqrt{3}+1$)×$\frac{\sqrt{3}}{2}$=$\frac{3+\sqrt{3}}{2}$.
∴四边形DEFC是矩形.
∴CD=EF=AB-AE+BF.
∵AE=ADcosA=$\sqrt{6}×\frac{\sqrt{6}-\sqrt{2}}{4}$=$\frac{3-\sqrt{3}}{2}$,BF=BCcos∠CBF=($\sqrt{3}+1$)×$\frac{1}{2}$=$\frac{\sqrt{3}+1}{2}$.
∴CD=1-$\frac{3-\sqrt{3}}{2}$+$\frac{\sqrt{3}+1}{2}$=$\sqrt{3}$.
故选:A.
点评 本题考查了解三角形,属于基础题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
1.若a=ln2,b=5${\;}^{-\frac{1}{2}}$,c=${∫}_{0}^{1}$xdx,则a,b,c的大小关系( )
| A. | a<b<cB | B. | b<a<cC | C. | b<c<a | D. | c<b<a |
19.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x+5},x≤0}\\{f(x-5),x>0}\end{array}\right.$,则f(2016)=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 16 | D. | 32 |