题目内容
13.求由曲线y=2-x2,直线y=x及x轴所围成的封闭图形的面积.分析 由题意作图象,从而结合图象,由定积分的几何意义即可求出.
解答 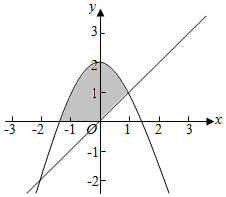 解:由$\left\{\begin{array}{l}{y=2-{x}^{2}}\\{y=x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-2}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
解:由$\left\{\begin{array}{l}{y=2-{x}^{2}}\\{y=x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-2}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
由y=2-x2,令y=0,解得x=-$\sqrt{2}$或x=$\sqrt{2}$,
∴由曲线y=2-x2,直线y=x及x轴所围成的封闭图形的面积为图中阴影部分的面积,
即为S=${∫}_{0}^{1}$(2-x2-x)dx+${∫}_{-\sqrt{2}}^{0}$(2-x2)dx+${∫}_{-2}^{-\sqrt{2}}$(2-x2-x)dx=$\frac{7}{2}$.
点评 本题考查了数形结合的思想应用及学生的作图能力,同时考查了定积分的应用.

练习册系列答案
相关题目